z
QWERTY:
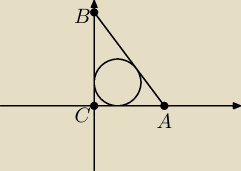
Trójkąt o wierzchołkach A(6,0) B(0,y) C(0,0) jest prostokątny. Oblicz y, jeżeli promień okręgu
wpisanego w ten trójkąt jest równy 2.
|CA|=
√36
|CB|=
√y2
|AB|=
√36+y2
CB
2+CA
2=AB
2 czemu nie wychodzi mi z tego
13 kwi 18:34
Adamm: Bo to tożsamość
13 kwi 18:46
Adamm:
Wzór na odległość dwóch punktów w układzie współrzędnych bierze się z twierdzenia Pitagorasa,
nie tędy droga
13 kwi 18:48
PW: Bez wykorzystania informacji o promieniu okręgu wpisanego "nie wyjdzie" − dla dowolnej liczby
y≠0 trójkąt jest prostokątny, twierdzenie Pitagorasa działa, ale nie pozwala wyliczyć y.
13 kwi 18:48
aniabb: czyli tradycyjnie Δ 6, 8, 10

13 kwi 22:22
Mila:
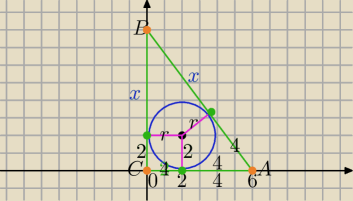
1) y=2+x
Punkty styczności okręgu wpisanego w Δ są jednakowo odległe od wierzchołków kątów.
2) tw. Pitagorasa
6
2+(2+x)
2=(4+x)
2
x=6
y=2+6=8
13 kwi 23:41
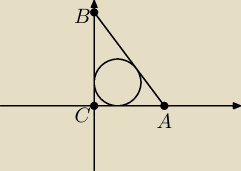 Trójkąt o wierzchołkach A(6,0) B(0,y) C(0,0) jest prostokątny. Oblicz y, jeżeli promień okręgu
wpisanego w ten trójkąt jest równy 2.
|CA|=√36
|CB|=√y2
|AB|=√36+y2
CB2+CA2=AB2 czemu nie wychodzi mi z tego
Trójkąt o wierzchołkach A(6,0) B(0,y) C(0,0) jest prostokątny. Oblicz y, jeżeli promień okręgu
wpisanego w ten trójkąt jest równy 2.
|CA|=√36
|CB|=√y2
|AB|=√36+y2
CB2+CA2=AB2 czemu nie wychodzi mi z tego

 1) y=2+x
Punkty styczności okręgu wpisanego w Δ są jednakowo odległe od wierzchołków kątów.
2) tw. Pitagorasa
62+(2+x)2=(4+x)2
x=6
y=2+6=8
1) y=2+x
Punkty styczności okręgu wpisanego w Δ są jednakowo odległe od wierzchołków kątów.
2) tw. Pitagorasa
62+(2+x)2=(4+x)2
x=6
y=2+6=8