zz Ale: Narysować zbiory liczb zespolonych:

	3
π < arg[(−1+i)z] ≤		π
	2

Nie wiem jak zmienić postać, żeby widać było co narysować.

piotr:

	3
π < arg[√2e3π/4 z] <		π
	2

	3
π − 3π/4 < arg[z] <		π − 3π/4
	2

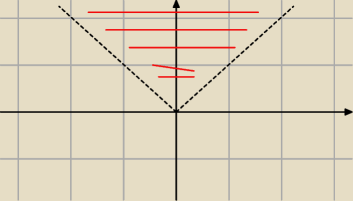
π/4 < arg[z] < 3π/4

Ale: Druga linijka, dlaczego z wykładnika 3π/4 przechodzi do sumy?

Ale: Nie bardzo rozumiem przejścia z pierwszej linijki do drugiej. Dziękuje za rysunek

PW:

	3
u=−1+i, a więc argu=		π (można po prostu narysować liczbę u − punkt (−1,1) na płaszczyźnie
	4

	3
zespolonej i zobaczyć, że argu=		π).
	4

Jeżeli oznaczymy argz=α, to

	3
arg(uz)=argu+argz=		π+a
	4

(mówiąc po chłopsku: mnożąc liczby zespolone otrzymujemy liczbę, której argument jest sumą argumentów mnożonych czynników). Mamy więc zilustrować nierówność

	3		3
π<		π+α<		π,
	4		2

czyli

	1		3
		π<α<		π
	4		4