optymalizacja johnik: dwa statki plyna stałym kursem wzdłuz linii prostych kursy obu statków przecinaja sie pod katem 120 stopni.w momencie gdy jeden z nich mijał punkt przeciecia sie tych kursów drugi znajdował sie "m" mil morskich przed nim. Po jakim czasie od tego momentu odleglosc miedzy statkami bedzie najmniejsza jezeli oba statki plyna z ta sama predkoscia. wyznacz te odlegosc rozważ DWA przypadki hmm, masakraa

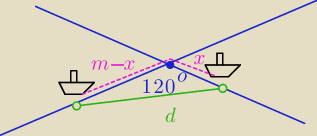
iteRacj@: d − odległość między statkami x − odległość statku drugiego od punktu przecięcia się kursów, 0≤x≤m z tw. cosinusów d²=(m−x)²+x²−2(m−x)²*cos120^o odległość między statkami jako funkcja odległości statku drugiego od punktu przecięcia się kursów f(x)=√(m−x)²+x²−2(m−x)²*cos120^o=√−x²−mx+m² funkcja f(x) przyjmie najmniejszą wartość, gdy funkcja podpierwiastkowa ma najmniejszą wartość policz pochodną, znajdź minimum funkcji drugi przypadek zostawiam Tobie

iteRacj@: miało być bez minusa f(x)=√x²−mx+m²

krzyśko: Te odległości od miejsca ich przecięcia będą m+x i x

ite: O dległości statków od punktu przecięcia się kursów (zaznaczony na granatowo kółkiem) to m−x oraz x. Suma odległości to musi być m. Wynika to z informacji: "w momencie gdy jeden z nich mijał punkt przecięcia się tych kursów drugi znajdował się "m" mil morskich przed nim" oraz z tego, że płyną z takimi samymi prędkościami. przy wpisywaniu tw. cosinusów dla odległości między statkami d źle przepisałam, powinno być: d²=(m−x)²+x²−2(m−x)*x*cos120^o i dalej f(x)=√(m−x⁾²+x²−2(m−x)²*cos120^o=√x²−mx+m²

johnik: tak, wiem , tylko jaki moze być drugi przypadek?

johnik: tylko choddzi mi o oznaczenie lub wytlumaczenie /

Pytający: Drugi przypadek: jeden ze statków płynie w przeciwną stronę niż w powyżej rozważanym przypadku (wtedy będziesz miał kąt 60^o).

johnik: a odleglosci, m+x i x

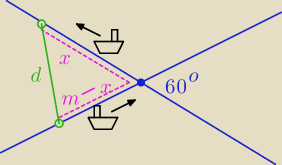
iteRacj@: drugi wariant podróży morskiej stałym kursem wzdłuż linii prostych d²=(m−x)²+x²−2(m−x)*x*cos 60^o

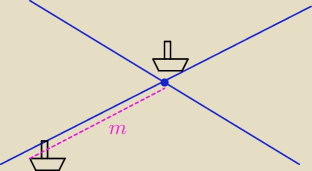
iteRacj@: suma odległości obu statków od punktu przecięcia się kursów (zaznaczony na granatowo kółkiem) nie zależy od kierunku poruszania i jest równa odległości początkowej m m=(m−x)+x dla 0≤x≤m

johnik:

	m
czyli dla takiego samego x=
	2

johnik: ?

iteRacj@:

	m
dla x=		odległość d między statkami będzie najmniejsza
	2