 Hej
Hej  Prosiłbym o wsparcie też w tym zadanku:
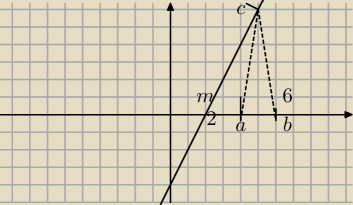
Dany jest punkt B=(6;0) i prosta o rownaniu y=2x−4 przecianjąca oś OX w punkcie M. T jest
trójkatem o najwiekszym polu wśród trójkątów równoramiennych takich, że wierzchołek kąta
prostego należy do odcinka BM, punkt B jest wierzchołkiem kąta ostrego, a trzeci wierzchołek
należy do danej prostej. Oblicz obwód trójkąta T.
Prosiłbym o wsparcie też w tym zadanku:
Dany jest punkt B=(6;0) i prosta o rownaniu y=2x−4 przecianjąca oś OX w punkcie M. T jest
trójkatem o najwiekszym polu wśród trójkątów równoramiennych takich, że wierzchołek kąta
prostego należy do odcinka BM, punkt B jest wierzchołkiem kąta ostrego, a trzeci wierzchołek
należy do danej prostej. Oblicz obwód trójkąta T.
 Wspołrzędne poszukiwanego punktu to C (x;2x−4)
wiem z B jest punktem z podstawy i że podstawa zamknieta jest w odcinku BM z czego M ma x=2
Nie wiem skąd mam wziąć wspołrzędne drugiego końca odcinka A, pan Kiełbasa stwierdza że x
∊<4;6) Nie wiem skąd się bierze ta 4 w dziedzinie bo w końcu M leży w punkcie 2 czyli chyba
2<x<6 (zakładając że x to wspólrzędne środka podstawy).
Bardzo proszę o pomoc
Wspołrzędne poszukiwanego punktu to C (x;2x−4)
wiem z B jest punktem z podstawy i że podstawa zamknieta jest w odcinku BM z czego M ma x=2
Nie wiem skąd mam wziąć wspołrzędne drugiego końca odcinka A, pan Kiełbasa stwierdza że x
∊<4;6) Nie wiem skąd się bierze ta 4 w dziedzinie bo w końcu M leży w punkcie 2 czyli chyba
2<x<6 (zakładając że x to wspólrzędne środka podstawy).
Bardzo proszę o pomoc  z góry dzięki. (odp. to 8)
z góry dzięki. (odp. to 8)
| 2*6 | ||
Jak tez nie wiem ... wskazany trojkat rownoramienny ma pole rowne | = 6 | |
| 2 |
| 4*4 | ||
Gdyby a= m to wtedy C(4,4) i pole rowne | = 8 czyli taki trojkat ma wieksze pole. | |
| 2 |

 Blee zgadzam się z Toba
Blee zgadzam się z Toba  wtedy mam 12x−24−2x2+4x=−24+16x−2x2
z tego pochodne 0+16−4x = P' no i przyrownać do 0 0=16−4x x=4 czyli h=4 czyli 16/2=8 no i
cacy.
To ta dzedzina, muszę ja rozgryźc jak będę miał pomysł, albo wiedział czemu to dam znać
wtedy mam 12x−24−2x2+4x=−24+16x−2x2
z tego pochodne 0+16−4x = P' no i przyrownać do 0 0=16−4x x=4 czyli h=4 czyli 16/2=8 no i
cacy.
To ta dzedzina, muszę ja rozgryźc jak będę miał pomysł, albo wiedział czemu to dam znać  A no i dzięki za zaangażowanie Blleee (gdybyś miał czas to proszę też o pomoc w tym zadanku:
https://matematykaszkolna.pl/forum/373553.html)
A no i dzięki za zaangażowanie Blleee (gdybyś miał czas to proszę też o pomoc w tym zadanku:
https://matematykaszkolna.pl/forum/373553.html)
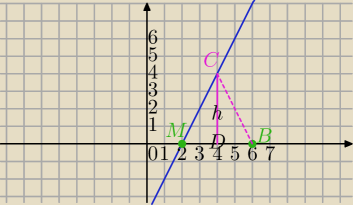 A=(a,0),a∊<2,6), B=(6,0)
C=(c,2c−4)
|AC|=|BC| ⇔√(c−a)2+(2c−4)2=√(c−6)2+(2c−4)2⇔
(c−a)2=(c−6)2
A=(a,0),a∊<2,6), B=(6,0)
C=(c,2c−4)
|AC|=|BC| ⇔√(c−a)2+(2c−4)2=√(c−6)2+(2c−4)2⇔
(c−a)2=(c−6)2
| a+6 | ||
a=6 ∉D lub c= | ||
| 2 |
| 1 | 1 | 1 | ||||
PΔ= | |AB|*h= | *(6−a)*(2c−4)= | *(6−a)*(a+2) | |||
| 2 | 2 | 2 |
| 1 | ||
P(a)= | *(−a2+4a+12) | |
| 2 |
| 1 | ||
P(2)= | *4*4=8− największe pole | |
| 2 |
 jest super, co prawda nie do konca chyba ten rysunek zgadza
sie z tym z odpowiedzi
jest super, co prawda nie do konca chyba ten rysunek zgadza
sie z tym z odpowiedzi  (bo ten z odpowiedzi jest taki jak narysowałem u góry), aleeee
według mnie to co piszesz brzmi mądrze i rozsądnie. Dziekuje Ci!
(bo ten z odpowiedzi jest taki jak narysowałem u góry), aleeee
według mnie to co piszesz brzmi mądrze i rozsądnie. Dziekuje Ci! 
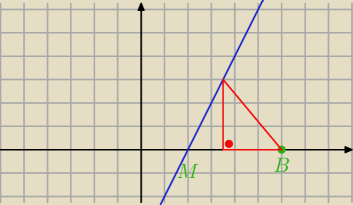 czy ja nie umiem czytać
czy ja nie umiem czytać bo trójkąt równoramienny prostokątny może być tylko jeden więc jakie
największe pole
bo trójkąt równoramienny prostokątny może być tylko jeden więc jakie
największe pole ..T jest trójkatem o najwiekszym polu wśród trójkątów równoramiennych takich, że wierzchołek
kąta prostego należy do odcinka BM, punkt B jest wierzchołkiem kąta ostrego, a trzeci
wierzchołek należy do danej prostej. ...
..T jest trójkatem o najwiekszym polu wśród trójkątów równoramiennych takich, że wierzchołek
kąta prostego należy do odcinka BM, punkt B jest wierzchołkiem kąta ostrego, a trzeci
wierzchołek należy do danej prostej. ...

