 Dzień dobry
Dzień dobry  Zadanie optymalizacyjne związane z planimetrią:
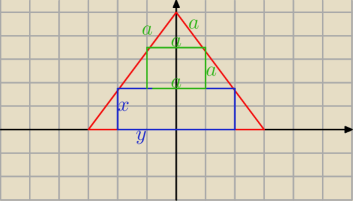
W trójkąt równoboczny, któego bok ma długość 2,, wpisujemy prostokąt i kwadrat. Jaka powina być
długosc boku kwadratu, jeżeli suma pól obu czworokąt ma być największa?
No nie wiem kurcze jak to zrobić
mam mieć a2+x*y
wiem że H trójkąta jest równe √3
wiem że ten najmniejszy trójkąt na szczycie kwdratu jest też rownboczny o bokach a;a;a czyli
Zadanie optymalizacyjne związane z planimetrią:
W trójkąt równoboczny, któego bok ma długość 2,, wpisujemy prostokąt i kwadrat. Jaka powina być
długosc boku kwadratu, jeżeli suma pól obu czworokąt ma być największa?
No nie wiem kurcze jak to zrobić
mam mieć a2+x*y
wiem że H trójkąta jest równe √3
wiem że ten najmniejszy trójkąt na szczycie kwdratu jest też rownboczny o bokach a;a;a czyli
| a√3 | ||
h= | ||
| 2 |
| a√3 | ||
Z tego wiem że x=√3− | −a | |
| 2 |
| 2√3−a√3+2a | ||
ale to wciąż za mało... żeby móc obliczyć wszystko mam a2+ | y, nie wiem jak | |
| 2 |
 Proszę o pomoc
Proszę o pomoc  Ps. Na necie znazłem to i to chyba biorą z podobieństwa... Tylko jak...
Ps. Na necie znazłem to i to chyba biorą z podobieństwa... Tylko jak...
| 9+8√3 | ||
https://www.matematyka.pl/196230.htm //ODP prawidłowa z ksiazki to : | ||
| 37 |
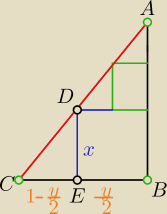 podpisalem wierzcholki zebys wiedzial ktore trojkaty sa podobne:
z podobienstwa trojkatow ABC i DEC
podpisalem wierzcholki zebys wiedzial ktore trojkaty sa podobne:
z podobienstwa trojkatow ABC i DEC
| |AB| | |DE| | ||
= | |||
| |BC| | |EC| |
| √3 | x | |||||||||||
= | ||||||||||||
| 1 |
|
 Dzieki za pomoc bardzo doceniam
Dzieki za pomoc bardzo doceniam