Optymalizacja, trapez, okrąg wpisany, geometria analityczna
Gustavo: Dany jest trapez równoramienny o kącie ostrym 45. Podstawy trapezu są równoległe do osi x,
wierzchołki krótszej podstawy należą do paraboli y=−x2−5x−2, a ramiona tego trapezu są
odcinkami stycznych do tej paraboli. Wyznacz współrzędne wierzchołków trapezu, wiedząć, że
można w niego wpisać okrąg.
10 kwi 19:51
Janek191:
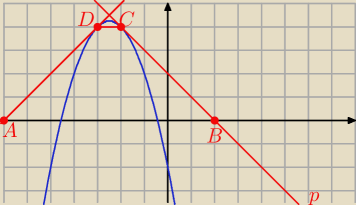
C = ( − 2, 4)
D = ( − 3, 4)
y = − x + b
4 = −1*(−2) + b ⇒ b = 2
y = − x + 2
oraz
y = x + k
4 = −3 + k ⇒ k = 7
y = x + 7
I C D I = −2 − (−3) = 1
oraz
I CD I + I AB I = 2* I BC I
1 + 2 x =
√( x +1)2 + ( 4 + x − 2)2
1 + 2 x =
√ x2 +2 x + 1 + 4 + 4 x + x2
1 + 4 x + 4 x
2 = 2 x
2 + 6 x + 5
2 x
2 − 2 x − 4 = 0
x
2 − x − 2 = 0
Δ = 1 − 4*1*(−2) = 9
√Δ = 3
10 kwi 20:29
Janek191:

C = ( − 2, 4)
D = ( − 3, 4)
y = − x + b
4 = −1*(−2) + b ⇒ b = 2
y = − x + 2
oraz
y = x + k
4 = −3 + k ⇒ k = 7
y = x + 7
I C D I = −2 − (−3) = 1
oraz
I CD I + I AB I = 2* I BC I
1 + 2 x =
√( x +1)2 + ( 4 + x − 2)2
1 + 2 x =
√ x2 +2 x + 1 + 4 + 4 x + x2
1 + 4 x + 4 x
2 = 2 x
2 + 6 x + 5
2 x
2 − 2 x − 4 = 0
x
2 − x − 2 = 0
Δ = 1 − 4*1*(−2) = 9
√Δ = 3
10 kwi 20:29
Gustavo: Okej, dzięki wielkie, jak rozumiem to do reszty powinienem dojsc samemu.
10 kwi 20:32
Janek191:
Poprawka
więc
B = ( 2, 0)
A = ( − 7, 0)
Jest gdzieś pomyłka

10 kwi 20:33
Gustavo: Tylko skąd wiadomo, że yc i yd to 4 będzie?
10 kwi 20:34
Gustavo: No własnie B i A powinno (−4−sqrt(2),3−sqrt(2)), (sqrt(2)−1, 3−sqrt(2)) wyjsc. Ale mi głównie
chodzi o to, skąd się bierze te 4 i skąd się biorą podane u mnie w odpowiedziach odcięte:
wskazuje, że w f'(x)=1 i f('x)=−1 są zawarte odcięte punktów, a nie wiem, skąd.
10 kwi 20:36
Janek191:
Poczatek
y ' = −2 x − 5 = tg 135o = − 1
więc
x = − 2
y = − 4 − 5*(−2) − 2 = 4
więc
C = ( − 2, 4)
Oś symetrii paraboli
x = −2,5
zatem symetryczny jest D = ( −3 , 4)
10 kwi 20:36
Gustavo: Ok, dzięki, nie wiedziałem, że tak można z trygonometrii dawać wartosci w pochodnej.
10 kwi 20:39
Janek191:
Pewnie powinno być ;
1 + 2 x + 2 √ ...
10 kwi 20:45
Janek191:
Pewnie powinno być ;
1 + 2 x + 2 √ ...
10 kwi 20:45
Janek191:
1 + 2 x = 2√ ...
10 kwi 20:46
Janek191:
Jednak jest źle od: wiersza następnego po:
I C D I + I AB I = 2 I BC I
10 kwi 20:48
Janek191:
B = ( x, − x + 2)
I A B i = 2 * ( x − (− 2,5)) = 2*(x +2, 5) =2 x + 5
10 kwi 20:52
Gustavo: Ok, dzięki.
10 kwi 21:28
 C = ( − 2, 4)
D = ( − 3, 4)
y = − x + b
4 = −1*(−2) + b ⇒ b = 2
y = − x + 2
oraz
y = x + k
4 = −3 + k ⇒ k = 7
y = x + 7
I C D I = −2 − (−3) = 1
oraz
I CD I + I AB I = 2* I BC I
1 + 2 x = √( x +1)2 + ( 4 + x − 2)2
1 + 2 x = √ x2 +2 x + 1 + 4 + 4 x + x2
1 + 4 x + 4 x2 = 2 x2 + 6 x + 5
2 x2 − 2 x − 4 = 0
x2 − x − 2 = 0
Δ = 1 − 4*1*(−2) = 9 √Δ = 3
C = ( − 2, 4)
D = ( − 3, 4)
y = − x + b
4 = −1*(−2) + b ⇒ b = 2
y = − x + 2
oraz
y = x + k
4 = −3 + k ⇒ k = 7
y = x + 7
I C D I = −2 − (−3) = 1
oraz
I CD I + I AB I = 2* I BC I
1 + 2 x = √( x +1)2 + ( 4 + x − 2)2
1 + 2 x = √ x2 +2 x + 1 + 4 + 4 x + x2
1 + 4 x + 4 x2 = 2 x2 + 6 x + 5
2 x2 − 2 x − 4 = 0
x2 − x − 2 = 0
Δ = 1 − 4*1*(−2) = 9 √Δ = 3
 C = ( − 2, 4)
D = ( − 3, 4)
y = − x + b
4 = −1*(−2) + b ⇒ b = 2
y = − x + 2
oraz
y = x + k
4 = −3 + k ⇒ k = 7
y = x + 7
I C D I = −2 − (−3) = 1
oraz
I CD I + I AB I = 2* I BC I
1 + 2 x = √( x +1)2 + ( 4 + x − 2)2
1 + 2 x = √ x2 +2 x + 1 + 4 + 4 x + x2
1 + 4 x + 4 x2 = 2 x2 + 6 x + 5
2 x2 − 2 x − 4 = 0
x2 − x − 2 = 0
Δ = 1 − 4*1*(−2) = 9 √Δ = 3
C = ( − 2, 4)
D = ( − 3, 4)
y = − x + b
4 = −1*(−2) + b ⇒ b = 2
y = − x + 2
oraz
y = x + k
4 = −3 + k ⇒ k = 7
y = x + 7
I C D I = −2 − (−3) = 1
oraz
I CD I + I AB I = 2* I BC I
1 + 2 x = √( x +1)2 + ( 4 + x − 2)2
1 + 2 x = √ x2 +2 x + 1 + 4 + 4 x + x2
1 + 4 x + 4 x2 = 2 x2 + 6 x + 5
2 x2 − 2 x − 4 = 0
x2 − x − 2 = 0
Δ = 1 − 4*1*(−2) = 9 √Δ = 3
