Wartości funkcji Michał: Po problemach z wartościami najmniejszymi, najwiekszymi czas na problem z obliczeniem wartości funkcji Podejrzewam że i tu ekstrema się przydadza aby obliczyć te największe/najmniejsze wartości funkcji

	x2
f(x)=
	(1+x)2

D_f: x+1=/=0 x=/=−1 Ok to proszę o pomoc co z tymi wartościami, z góry dzięki za pomoc

Michał:

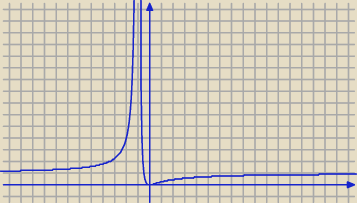
Janek191: Asymptota pionowa x = − 1, więc brak wartości największej. y_min = 0

Janek191: Oblicz granice w −∞ i w +∞ oraz granice jednostronne w − 1.

Michał: Ok, czyli rysowanie funkcji jedynym wyjściem dzieki Janek za czas =)

tytyryty: Równoważne polecenie: Rozwiąż równanie f(x) = m, w zależności od wartości parametru m.

the foxi:

	x
Hmmm, można też zauważyć, że f(x)=(		)2
	1+x

a jak wiadomo, cokolwiek podniesione do kwadratu jest większe bądź równe zero − to może pomóc

Michał:

x2
(1+x)2

	12
limn−>1+		=1/2 analogicznie dla 1−
	1+1

lim_n−>+oo −||−=1 Analogicznie dla −oo lim_n−>−1⁺ −||− >0 lim _n−>−1⁻ −||− >0 czyli w tych dwóch chyba +oo co do stwierdzenia z parametrem to jak by to trzeba było wtedy rozwiazac X_x the foxi racja z tym kwadratem, choć oprócz stwierdzenia że wszystko bedzie >0 chyba nic mi to nie daje

the foxi: Nie zawsze, ale w tym przypadku tak − jeśli znajdziesz argument, dla którego f(x)=0, to automatycznie oznacza, że to jest najmniejsza wartość

Michał: Mmm sprytne dzieki za radę

tytyryty: Wracając do parametru:

x2
	= m
(1+x)2

przekształcając mamy: (m+1)x² + 2mx + m = 0 i teraz sprawdzasz dla jakich wartości m to równanie ma co najmniej jedno rozwiązanie. czyli masz do rozpatrzenia 2 przypadki: (1) gdy m=−1 (2) gdy m ≠ −1 (tutaj po prostu sprawdzasz dla jakich m Δ ≥ 0) Suma rozwiązań (1) i (2) daje zbiór wartości f.

Michał: kurcze panowie/panie nie wiem skąd wy bierzecie na to pomysły, ale to genialne ... Dzięki tyryryty, na prawdę fajne podejście o tym też nie pomyślałem w ten sposób dziękuję