W trójkąt prostokątny wpisano okrąg. Punkt styczności przeciwprostokątnej... KomosaRyżowa: W trójkąt prostokątny wpisano okrąg. Punkt styczności przeciwprostokątnej z okręgiem dzieli ją na odcinki o długościach x i y. Wykaż, że pole trójkąta jest równe xy. Doszłam do tego, że: Pole trójkąta mogę policzyć na dwa sposoby:1/2(x+r)(y+r) oraz pr=r(x+y+r) (gdzie p to połowa obwodu) Prawdopodobnie gubię się gdzieś w obliczeniach, bo powinno wyjść z powyższego. Pomoże ktoś?

KomosaRyżowa: Dobra, ogarnęłam, zaraz wrzucę rozwiązanie jakby ktoś coś kiedyś potrzebował

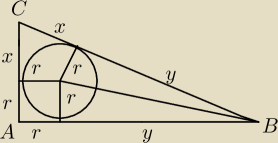
KomosaRyżowa: Pole trójkąta na dwa sposoby: 1/2(x+r)(y+r) lub pr=r(x+y+r) (gdzie p to połowa obwodu) Porównujemy: r(x+y+r)=1/2(x+r)(y+r) 2r(x+y+r)=(x+r)(y+r) 2rx+2yr+2r²=xy+xr+yr+r² xr+yr+r²=xy L=pole trójkąta P=xy Pole trójkąta=xy cnp.

Darek: