Geometria w przestrzeni
Tomek: W dwa przeciwległe naroża sześcianu o danej krawędzi a wpisano dwie równe kule
wzajemnie styczne. Obliczyć odległość środków tych kul.
| | a(3−√3) | |
Odpowiedz książkowa to : |
| |
| | 2 | |
Patrząc na przekrój zawierający przekątna podstawy a
√2 i wysokość a można ułożyć równanie:
(2R)
2 = (a−2R)
2 + (a
√2−2R)
2
Czy dobrze rozumuje?
Wynik wychodzi mi inny.
Możecie zrobić to zadanie i napisać jaki macie wynik? Dziękuje
9 kwi 23:46
Blee:
jak dla mnie to:
R
2 + R
2 = (R+x)
2 (mały trójkąt prostokątny)
a
2 + a
2 = (4R + 2x)
2 (przekątna kwadratu)
9 kwi 23:57
Tomek: Tak napewno nie. Jak spojrzysz na sześcian w taki sposób to kule najda na siebie.
Widok który pokazuje styczne kule to płaszczyzna zawierająca przekątna podstawy kwadratu i
wysokość a
10 kwi 00:02
Tomek: Krótko mówiąc promienie kul nie zawierają się w przekątnej sześcianu
10 kwi 00:04
10 kwi 00:15
Mila:
iteRacj@ niezawodna.
Dodam rysunek.
10 kwi 21:38
Mila:
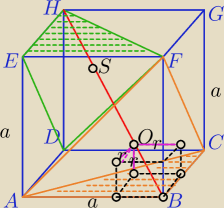
1) Kula wpisana w naroże B jest styczna do 3 ścian sześcianu mających wspólny wierzchołek B⇔
środek O jest oddalony od każdej z tych ścian o długość promienia r.
Odległość środka kuli od wierzchołka B jest równa r*
√3 ( przekątna sześcianu o krawędzi r)
To samo dotyczy kuli wpisanej w naroże H.
2)
|OS|=2r ponieważ kule są styczne.
3)
a
√3=2*r*
√3+2r
a*
√3=2r*(
√3+1)
================
11 kwi 23:17
