stereo
mk: Podstawa ostrosłupa jest trójkąt równoramienny, w którym boki równe mają długość b, a kąt
między nimi zawarty jest równy α. Oblicz objętość ostrosłupa jeśli każda krawędź boczna tworzy
z wysokością ostrosłupa kąt β. Obliczyłam trzeci bok w podstawie ostrosłupa a=b√2−2cosα i w
internecie wyczytałam, że spodek ostrosłupa pokrywa się ze środkiem okręgu opisanego na
podstawie ostrosłupa. Może mi ktoś yjaśnić skąd wiadomo, że te punkty si pokrywają? Z resztą
sobie poradze.
9 kwi 22:52
Mila:
"każda krawędź boczna tworzy z wysokością ostrosłupa kąt β."⇒Każda krawędź boczna tworzy
z płaszczyzną podstawy kąt (90−β)⇔
że spodek ostrosłupa pokrywa się ze środkiem okręgu opisanego na podstawie.
9 kwi 23:13
mk: Wciąz nie rozumiem, ale dzięki za próbe wytłumaczenia.
9 kwi 23:18
Mila:
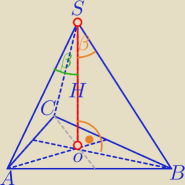
H=SO − prostopadłe ( jako wysokość) do płaszczyzny ABC
ΔSOB≡ ΔSOA≡SOC −Δprostokątne− wspólna przyprostokątna i jeden kąt ostry równy, to drugi też .
⇔|OB|=|OA|=|OC|⇔
punkt O jest jednakowo odległy od wierzchołków ΔABC⇔jest środkiem okręgu opisanego na tym Δ
9 kwi 23:36
mk: Ok już kumam, dziękuje bardzo!
9 kwi 23:59
Mila:

10 kwi 00:16
 H=SO − prostopadłe ( jako wysokość) do płaszczyzny ABC
ΔSOB≡ ΔSOA≡SOC −Δprostokątne− wspólna przyprostokątna i jeden kąt ostry równy, to drugi też .
⇔|OB|=|OA|=|OC|⇔
punkt O jest jednakowo odległy od wierzchołków ΔABC⇔jest środkiem okręgu opisanego na tym Δ
H=SO − prostopadłe ( jako wysokość) do płaszczyzny ABC
ΔSOB≡ ΔSOA≡SOC −Δprostokątne− wspólna przyprostokątna i jeden kąt ostry równy, to drugi też .
⇔|OB|=|OA|=|OC|⇔
punkt O jest jednakowo odległy od wierzchołków ΔABC⇔jest środkiem okręgu opisanego na tym Δ
