ciągi Michał: Dobry wieczór Tym razem pytanie typu sprawdź: KOrzystajc z defincji pochodnej funkcji w punkcie, czy istnieje pochodna funkcji f w punkcie x₀=0 f(x)=|2x| Nie wiem jak poradzić sobie z tą wartością bezwględną Jezeli mam jakieś pomysły poddać to cos z definicją kombinuje {2x dla x>=0 |2x|= { {−2x dla x<0

Mila:

	f(x0+h)−f(x0)
limh→0+		=
	h

	|2*(0+h)|−2*0		2h
= lim h→0+		=		=2
	h		h

	f(0+h)−f(0)
limh→0−		=
	h

	|2*(0+h)|−2*0		2(−h)
= lim h→0−		=		=−2
	h		h

Nie istnieje pochodna f(x) w x₀=0 ========================

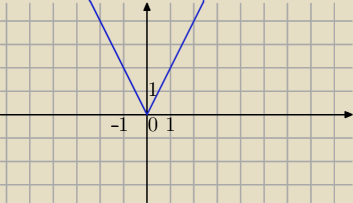Mila: W x₀=0 masz "szpic", tu funkcja nie ma pochodnej.

Michał: Hmn, dziękuję Milo za rozwiązanie, choć mam pytanie po zastoswaniu tego wzorku obliczasz lim h→0⁺ i otrzymuje 2h/h h to toszkę wiecej niz 0 czyli liczba dodatnia... potem to samo robisz dla h→0⁻ i wychodzi Ci:

2(−h)
	Czemu tak przecież to są te same obliczenia co wyżej z tą różnicą że h to chyba
h

toszku mniej niż 0 czyli liczba ujemna. No ale wtedy, czemu nie ma miinusa też w mianowniku? Damn, przepraszam za problemy które sprawiam, bo bardzo fajnie jest to rozpisane, choć ten jeden kork mi umyka a chciałbym to zrozumieć.

Mila: Licznik jest w wartości bezwzględnej a mianownik nie.

Michał: Ah, ok dziękuję Mila, nie wziąłem tego pod uwagę Dzięki za cierpliwość i rozpisanie <3

Mila: