pomocy
sinus: Przez przekatna dolnej podstawy prostopadloscianu i jeden z jego gornych wierzcholkow
poprowadzono plaszczyzne. Przekroj jest trojkatem o dwoch bokach dlugosci 2 i 3 oraz kacie
miedzy nimi rownym 60 stopni. Oblicz objetosc prostopadloscianu oraz sinus kata nachylenia
plaszczyzny przekroju do podsawy
9 kwi 20:10
iteRacj@:
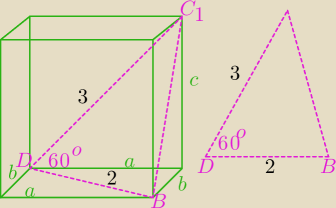
z tw.cosinusów w ΔDBC
1
|C
1B|
2=3
2+2
2−2*3*2*cos 60
o=9+4−6=7
a
2+b
2=2
2
c
2+b
2=7
a
2+c
2=3
2
z tego układu wyliczamy
a=1 b=
√3 c=
√6
V=a*b*c=1*
√3*
√6
9 kwi 21:39
Mila:
Podaj odpowiedź. Ja nieco inaczej ustaliłam długości boków.
Objętość mam taką samą.
Chodzi mi o sinus kąta nachylenia.
9 kwi 21:53
Mila:
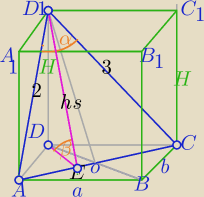
α=60
o
1) |AC|
2=2
2+3
2−2*2*3 *cos60
o
|AC|
2=7⇔|AC|=
√7
2)
a
2+b
2=7
a
2+H
2=3
2
b
2+H
2=2
2
−−−−−−−−−−−−−− stąd
a
2−b
2=5 i a
2+b
2=7
a=
√6, H=
√3, b=1
3) V=
√6*1*
√3=
√18=3
√2
V=3
√2
=====
4) β−Kąt nachylenia płaszczyzny ACD1
| | 1 | | 3√3 | |
PΔACD1= |
| *2*3*sin60= |
| |
| | 2 | | 2 | |
| | 1 | | 1 | | 3√3 | |
PΔACD1= |
| *|AC|*h⇔ |
| *√7*h= |
| |
| | 2 | | 2 | | 2 | |
=============
9 kwi 21:58
iteRacj@:
moim zdaniem ten prostopadłościan może "leżeć" na dowolnym boku, stąd objętość taka sama, ale
krawędzie inaczej przypisane
9 kwi 21:59
iteRacj@:
| | 2√2 | |
u mnie sinus kąta nachylenia |
| |
| | 3 | |
9 kwi 22:04
Mila:
Też bliski 1.
9 kwi 22:08
iteRacj@:
ten trzeci sinus wychodzi mi równy 1
9 kwi 22:15
 z tw.cosinusów w ΔDBC1
|C1B|2=32+22−2*3*2*cos 60o=9+4−6=7
a2+b2=22
c2+b2=7
a2+c2=32
z tego układu wyliczamy
a=1 b=√3 c=√6
V=a*b*c=1*√3*√6
z tw.cosinusów w ΔDBC1
|C1B|2=32+22−2*3*2*cos 60o=9+4−6=7
a2+b2=22
c2+b2=7
a2+c2=32
z tego układu wyliczamy
a=1 b=√3 c=√6
V=a*b*c=1*√3*√6
 α=60o
1) |AC|2=22+32−2*2*3 *cos60o
|AC|2=7⇔|AC|=√7
2)
a2+b2=7
a2+H2=32
b2+H2=22
−−−−−−−−−−−−−− stąd
a2−b2=5 i a2+b2=7
a=√6, H=√3, b=1
3) V=√6*1*√3=√18=3√2
V=3√2
=====
4) β−Kąt nachylenia płaszczyzny ACD1
α=60o
1) |AC|2=22+32−2*2*3 *cos60o
|AC|2=7⇔|AC|=√7
2)
a2+b2=7
a2+H2=32
b2+H2=22
−−−−−−−−−−−−−− stąd
a2−b2=5 i a2+b2=7
a=√6, H=√3, b=1
3) V=√6*1*√3=√18=3√2
V=3√2
=====
4) β−Kąt nachylenia płaszczyzny ACD1