Zadanie optymalizacyjne z trójkątem Paweł: Rozpatrujemy trójkąty o obwodzie L i jednym z kątów równym 120^o. Oblicz długości boków tego trójkąta, dla którego pole koła wpisanego w ten trójkąt będzie największa. Głowię się nad tym już od dłuższego czasu i nie mogę znaleźć równania funkcji P(L).

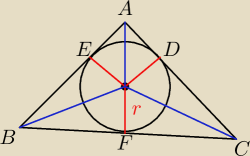
an: AC=x AD=AE=r*ctg60_o CD=CF BE=BF=(l−(2x −AD)−AE) S=p*r=r*l/2 S=|AB|*|AC|*sin120_o ⇒ r=f(x) ⇒ obliczamy max f(x)

an: S=0,5|AB|*|AC|*sin120^o

Paweł: A przypadkiem nie będzie tak, że BE=BF=(l−2x)/2?