Oblicz miarę kąta xx: Kąt między krawędziami przeciwległych ścian bocznych ostrosłupa prawidłowego czworokątnego ma miarę mniejszą o 10 ° od miary kąta między krawędzią boczną a podstawą. Oblicz jego miarę.

aniabb:

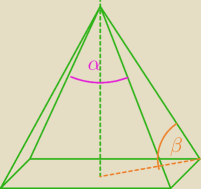
iteRacj@: aniabb czy α to jest ten kąt między krawędziami przeciwległych ścian bocznych czy nie?

iteRacj@: u Ciebie 13:28 jest narysowany przekrój zawierający przekątną podstawy?

aniabb: to przekrój.. wzięłam jedną krawędź z jednej ściany i inną z drugiej

aniabb: wolfram mówi że to jakieś 25° czyli 24,8342649°

aniabb: a jednak 46,256 °

xx: Zgubilam się i nadal nie rozumiem jak to rozwiązać.

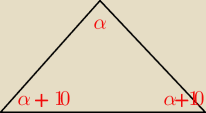
iteRacj@: na podstawie rysunku anibb z 13:28 α+α+10^o+α+10^o=180^o // suma kątów w trójkącie

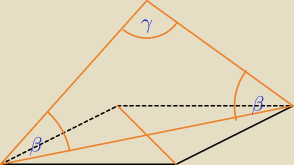
Bogdan: Angażować wolfram do takiego zadania? β = γ + 10^o 2β + γ = 180^o

Eta:

aniabb: wolframa używałam do rysunku iteRacj@ bo chyba jednak miała rację, że do kąta między ścianami trzeba używać tych samych krawędzi

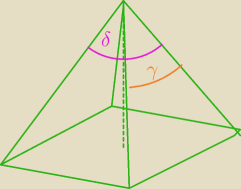
iteRacj@: dla mnie treść zadania była niejednoznaczna miałam wątpliwość, bo wydawało mi się, że kąt między krawędziami przeciwległych ścian bocznych ostrosłupa to może być zarówno δ jak i γ wiedziałam o które ściany chodzi, ale o które krawędzie już nie

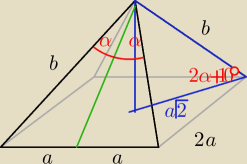
aniabb: sinα=a/b cos(2α+10)=a√2/b więc cos(2α+10)=√2sinα i z wolframa szukany kąt 2α=46,256°

aniabb: chociaż jeśli te obok to zazwyczaj nazywają krawędzie ściany bocznej nie musieliby dopisywać przeciwległe

aniabb: chyba że specjalnie chcieli namieszać