trójkąty Qba: 1) W trójkącie prostokątnym ABC poprowadzono wysokość CD z wierzchołka kąta prostego Okrąg którego średnicą jest DC odcina na przyprostokątnych odcinki o długościach m i n

	(m2+n2)2
Wykaż,że pole trójkąta ABC jest równe
	2mn

2) Dany jest trójkąt ABC w którym |∡ACB|=60⁰ i |BC|<|AC| Na boku AC obrano punkt M tak,że |AM|=|BC| Punkt N jest punktem symetrycznym do punktu B względem punktu C Wykaż że |MN|=|AB|

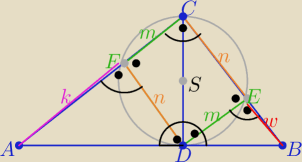Eta: 1/ jak zawsze... przejrzysty rysunek zgodny z treścią zadania i odpowiednie oznaczenia 2/ P(ABC)= P(DECF)+P(ADF)+P(BDE) P(ADECF)= mn

	n2		1		n3
WΔADC : n2=k*m ⇒k=		to P(ADF)=		*k*n =
	m		2		2m

	m2		1		m3
w ΔDBC: m2= w*n ⇒ w=		to P(BDE )=		*w*m =
	n		2		2n

	n3		m3		n4+2m2n2+n4		(m2+n2)2
zatem P(ABC)=mn+		+		=		=
	2m		2n		2mn		2mn

c.n.w

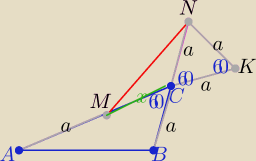Eta: zad2/ 1/ rysunek .... oznaczenia .... zgodne z trescią 2/ dorysowuję trójkąt równoboczny CNK o boku "a" teraz tylko należy wykazać,że trójkąty ABC i MNK są przystające |AC|=a+x=|MK|=a+x i |BC|=|NK|=a i kąt BC=kąt MKN=60^o z cechy (bkb) trójkąty są przystające zatem |AB|=|MN| c.n.w

Qba: Wieeeeeeelkie dzięki Eta