Sterometria problem Grzechu: zad1 stożek o wysokości 1 przecięto płaszczyzną równoległą do płaszczyzny podstawy. Pole otrzymanego przekroju jest dwa razy mniejsze od pola podstawy. wyznacz odległość przekroju od wierzchołka stożka zad2 w ostrosłupie prawidłowym trójkątnym krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem 30. Wyznacz cosinus kąta nachylenia ściany bocznej do płaszczyzny podstawy. Wyszedł mi zły wynik. zad3 w ostrosłupie prawidłowym czworokątnym abcds o podstawie abcd, kąt dwuścienny między płaszczyzna ściany bocznej i płaszczyzną podstawy ma miarę 30 . Odcinek łączący spodek wysokości ostrosłupa ze środkiem wysokości SE ściany bocznej ma długość 6. Oblicz objętość ostrosłupa. Dzięki z góry za pomoc.

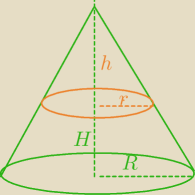
iteRacj@: zad. 1 h=? πR²=2πr² , r>0, R>0 √2r=R

h		H		h		1
	=				=
r		R		r		√2r

Grzechu: Skąd to twierdzenie że pole podstawy musi być równe obwodowi przekroju?

aniabb: to z treści zadania że: Pole otrzymanego przekroju jest dwa razy mniejsze od pola podstawy

iteRacj@: z treści zadania: Pole otrzymanego przekroju jest dwa razy mniejsze od pola podstawy. zapisałam to jako 2πr² = πR²

iteRacj@:

Grzechu: aaa sry pomieszało mi się strasznie.. Dobra jedno z głowy , Dzięki

iteRacj@: jedno z głowy czy o jedno bliżej do matury?

Grzechu: Niestety to drugie

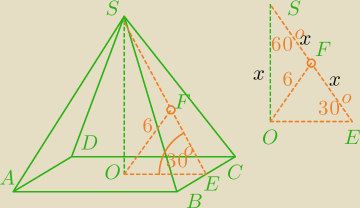
iteRacj@: x=|SO|=|SF|=|FE| → ΔSOF równoboczny więc x=|SO|=6, |SE|=12, |OE|=√3*6 P_ABCD=(2|OE|)²

	1
V=		*PABCD*|SO|=...
	3

Grzechu: Dzięki, zostało ostatnie. 😍