Tales xyz: Dany jest trójkąt prostokątny ABC o kącie prostym przy wierzchołku B. Do boków AB i BC dobudowano odpowiednio kwadraty BCDF oraz ABFG. Prosta AD przecięła bok BC w punkcie I natomiast prosta CG bok AB w punkcie H. Wykaż ze HB = BI.

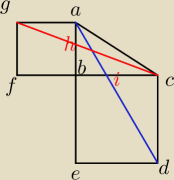
Basia: x = |AB| y = |BC|

	x
trójkąt ABI jest podobny do AED w skali
	x+y

	x		x*y
stąd |BI| = y*		=
	x+y		x+y

	y
trójkat HBC jest podobny do GFC w skali
	y+x

	y		x*y
stąd |HB| = x*		=
	y+x		x+y

co kończy dowód

xyz: Dziękuję