Proszę o rozwiązania, nie mam pojęcia gdzie popełniam błędy :/ 1251290: Zad. 1 Zbadać zbieżność bezwzględną i warunkową szeregu n=1 do ∞ ∑(−1)ⁿ⁺¹ * n / (n+1) Zad. 2 Wyznaczyć dziedzinę i asymptoty funkcji f(x) = √x² + x + x Zad. 3 Z de L'Hospitala obliczyć granice: a) dla x −> 1 (x/(x−1) − 1/(lnx)) b) dla x −> 0+ (cosx)^1/x2 Zad. 4 Wyznaczyć dziedzinę, przedziały monotoniczności i ekstrema lokalne funkcji f(x) = x² * e^1/x2

Basia: ad.1 bezwzględnie zbieżny nie jest, bo masz wtedy

1		2		3		1		1		1		1
	+		+		+...... >		+		+		+.... = ∑n=1.....
2		3		4		2		3		4		n

a to jest szerg harmoniczny rozbieżny bez wartości bezwzględnej masz

1		2		3		4		2k−1		2k
	−		+		−		+.....+		−		+...... =
2		3		4		5		2k		2k+1

3		4		15		16		(2k−1)(2k+1)		2k*2k
	−		+		−		+....+		−		+.... =
6		6		20		20		2k(2k+1)		2k(2k+1)

	1		1		1
−		−		− ..... −		− ................. =
	6		20		2k(2k+1)

	1		1
−∑k=1......		= −∑k=1.....
	2k(2k+1)		4k2+2k

1		1
	<
4k2+2k		4k2

	1
czyli szereg ∑k=1....		jest zbieżny bo
	4k2+2k

	1
∑k=1....		jest zbieżny
	4k2

	1
to znaczy, że ∑k=1....		= g (g jest liczbą skończoną)
	4k2+2k

	1
stąd −∑k=1....		= −g (−g też jest liczbą skończoną)
	4k2+2k

czyli szereg jest warunkowo zbieżny

jc: Szereg rozbieżny bo wyraz ogólny nie jest zbieżny do zera (w ogóle nie jest zbieżny).

1251290: Dziękuję serdecznie, widzę że twoje rozwiązanie różni się od mojego, ja przy sprawdzaniu zbieżności bezwzględnej założyłem moduł na to, co pod znakiem sumy i porównałem to z szeregiem 1/n, alfa(potęga liczby n) =1 czyli szereg na pewno nie jest zbieżny bezwzględnie. W przypadku warunkowej zbieżności użyłem kryterium Leibnitza , pokazując że n / n+1 ma wyrazy dodatnie, jest malejący oraz ma granicę w 0, zatem szereg (−1)ⁿ+1 (n / n+1) jest zbieżny warunkowo, widzisz w moim rozumowaniu jakiś błąd?

Basia:

	n
jc jak liczysz granicę (−1)n+1		?
	n+1

wiem, że ona w ogóle nie istnieje bo mamy podciąg zbieżny do 1 i podciąg zbieżny do −1 ale ten szereg daje się zapisać wzorem

	k		k+1		k2+2k−k2−2k−1
∑k=1,3,5.... [		−		] = ∑k=1,3,5...		=
	k+1		k+2		(k+1)(k+2)

	−1
∑k=1,3,5....
	k2+3k+2

	1
a szereg ∑k=1,3,5...		jest zbieżny
	k2+3k+2

Basia: aby skorzystać z kryterium Leibnitza musisz mieć lim_n→+∞a_n = 0

	n		1		1
limn→+∞		= limn→+∞		=		= 1
	n+1		1   1+   n		1+0

	n
poza tym ciąg an =		jest rosnący
	n+1

	n+1		n		n2+2n+1−n2−2n		1
an+1−an =		−		=		=		> 0
	n+2		n+1		(n+1)(n+2)		(n+1)(n+2)

Adamm: skoro granica nie istnieje to szereg jest rozbieżny więc coś Basiu robisz źle

Adamm: no teraz już widzę nieuzasadnione jest łączenie szeregów wyrazami tak jak to zrobiłaś

Adamm: 2. √x²+x+x≈√(x+1/2)²+x=|x+1/2|+x w ∞ będzie 2x+1/2 w −∞ będzie −1/2

Basia: wiem, to jest sprzeczność, ale nie wiem na czym tutaj polega błąd chodzi mi o to łączenie wyrazów o przeciwnych znakach, dlaczego to daje taki dziwaczny wynik?

Adamm: dlaczego a_n→0 gdy ∑a_n jest zbieżny? S_n+1−S_n→0 z tw. o różnicy ciągów zbieżnych więc skoro (−1)ⁿ*n/(n+1) jest rozbieżny, to automatycznie musi być ∑a_n

Adamm: bo to jest jakby podciąg o wyrazach parzystych, a ty badasz cały ciąg

Adamm: dlatego nie wolno sobie tak łączyć w pary wyrazów mówimy czasami że szeregi nie mają własności łączności

Basia: tak teraz widzę tak jak w najprostszym szeregu naprzemiennym ∑(−1)ⁿ S_2k = 0 dla każdego k S_2k+1 = −1 dla każdego k każdy jest sam w sobie zbieżny, razem nie łączenie wyrazów jest uprawnione tylko przy skończonej ich liczbie

Adamm: Tzn. można łączyć je w pary kiedy szereg jest o wyrazach dodatnich

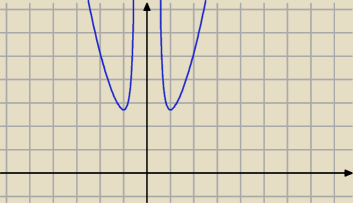
Basia: ad.4 f(x) = x²*e^1/x2 x≠0 D_f = R\{0}

	1
f'(x) = 2x*e1/x2 + x2*e1/x2*(−		*2x) =
	x4

	2		x2−1
e1/x2*[ 2x −		] = 2*e1/x2*
	x		x

f'(x)=0 ⇔ x²−1=0 ⇔ x=−1 ∨ x=1 x∊(−∞;−1) ⇒ f'(x) <0 ⇒ f ↘ x∊(−1;0) ⇒ f'(x)>0 ⇒ f↗ x∊(0;1) ⇒ f'(x)<0 ⇒ f↘ x∊(1;+∞) ⇒ f'(x)>0 ⇒ f↗ funkcja ma dwa minima lokalne x_min1 = −1 f₍−1) = 1*e¹ = e x_min2 = 1 f(1) = 1*e¹ = e

Basia: ad.3a

	x		1		x*ln(x) − x+1
limx→1 [		−		] = limx→1		=
	x−1		lnx		(x−1)*ln(x)

	1*0−1+1
[		] = (H)
	0*0

	1   ln(x) + x* − 1   x		ln(x)
limx→1		= limx→1		=
	x−1   ln(x) +   x		x−1   ln(x)+   x

	ln1		1   x
[		] = (H) = limx→1		=
	0   ln1 +   1		1   1   + x   x2

	1   x		1		x2		x
limx→1		= limx→1		*		= limx→1		=
	x+1   x2		x		x+1		x+1

	1
	2

Basia: ad.3b f(x) = (cosx)^1/x2

	1		ln(cosx)
limx→0+ln(f(x)) = limx→0+		*ln(cosx) = limx→0+		=H
	x2		x2

	1   *(−sinx) cosx		tgx
limx→0+		= −limx→0+		= (H)
	2x		2x

	1   cos2x		1		1
−limx→0+		= −limx→0+		= −
	2		2cos2x		2

	1
stąd limx→0+ f(x) = e−1/2 =
	√e