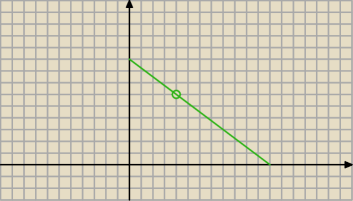
Optymalizacja Blabla: Prosta przechodząca przez punkt P(4,6) przecina dodatnie półosie układu współrzędnych w punktach A i B. Wyznacz wspolczynnik kierunkowy tej prostej tak, aby trójkąt ABO (gdzie punkt O jest początkiem układu współrzędnych) miał najmniejsze pole. Więc tak... Rysunek narysowalem, obliczyłem że A(0, 6−4a) B(4a−6/a, 0), obliczyłem z tego pochodną i teraz jest problem. Czemu mam ją przyrównywać do zera i co z tego będę mial? Chodzi mi o zrozumienie 🙂

Basia:

	(6−4a)(4a−6)		−(4a−6)2		−16a2+48a−36		18
P =		=		=		= −8a+24−
	2a		2a		2a		a

pole jest funkcją zmiennej a szukasz minimum tej funkcji a funkcja ma ekstrema tam gdzie jej pochodna = 0 i zmienia znak dlatego liczysz pochodną, przyrównujesz ją do zera i sprawdzasz czy następuje zmiana znaku i z jakiego na jaki aby było minimum musi być zmiana z (−) na (+)

Tadeusz: policzysz a dla którego S_min

Blabla: ekstrema.... dobra już Teraz rozumiem, wielkie dzięki 😅∊