Kąt dwuścienny w ostrosłupie Paula: Hej. Stereometria. Jest ostrosłup czworokątny o podstawie będącej prostokątem o bokach 4 i 4√2 , krawędzie boczne wszystkie mają długość 4. Obliczyć trzeba cosinus kąta zawartego między ścianami bocznymi tego ostrosłupa. Policzyłam przekątną podstawy, jeden "bok" kąta to wysokość trójkąta równobocznego, drugi policzyłam z tw. cosinusów bo trójkąt jest prostokątny równoramienny. Podstawiłam to wszystko do tw. Cosinusów i .... @&%$#, nie zgadza się z odpowiedzią rachunki sprawdzałam i ja , i druga osoba niezależnie. Błędu nie ma. Co robię źle?

Ariusz : Jaki jest wynik ?

Paula: Według odpowiedzi −√3/3

Ariusz : No i tak mi wyszło, zobacz, że masz jeden trójkąt równoboczny a drugi to równoramienny. Gdy obliczysz dwie wysokości tych trójkątów wykorzystujesz twierdzenie cos i masz wynik

Paula: Moja wyobraźnia przestrzenna coś niedomaga, chyba źle ten kąt widzę

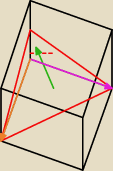
Ariusz : Zielona strzałka ten kąt długość różowego 4 pomarańczowego 4 √2 Oblicz wszystkie boki tego trójkąta a następnie cos z tw. cos

Ariusz : Teraz juz dasz radę ?

Mila: Trzeba zrobić dobry rysunek.

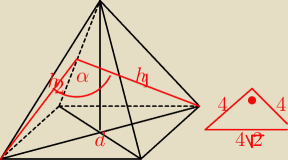
Basia: szukasz kata α h₂ to wysokość trójkąta równobocznego o boku 4 h₁ to wysokość trójkąta równoramiennegio 4,4,4√2 opuszczona na jego ramię h₁ = 4; trójkąt 4,4,4√2 jest prostokątny czyli mamy

	4√3
h2 =		= 2√3
	2

h₁ = 4 d = 4√3 i twierdzenie cosinusów

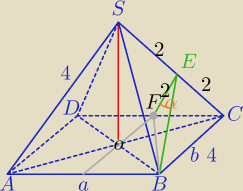
Mila: a=4√2, b=4 1) ΔBCS− Δrównoboczny, rzutem prostokątnym p.B na SC jest środek tej krawędzi 2) ΔDSC jest trójkątem równoramiennym i prostokątnym, ∡DSC=90^o, rzutem punktu D na Sc jest punkt S ( Nie ma Δ) Przesuwamy równoległe krawędź DS 3) |BE|=2√3,| FE|=2 ( Tales) F− środek DC, |FB|²=(2√2)²+4²=24 4) W ΔFBE: |FB|²=2²+(2√3)²−2*2*2√3*cosα 24=16−8√3 cosα

	√3
cosα=−
	3

=============

Paula: Bardzo wam wszystkim dziękuję!

Mila: Myślałam, że już tu nie spojrzysz. Ten kąt prosty podstępny.

Paula: A szczególnie Mili!

Mila: Skoro jesteś, to napisz skąd to zadanko?

Paula: "TERAZ MATURA" poziom rozszerzony z Nowej Ery

Mila: Dziękuję. Owocnej nauki!