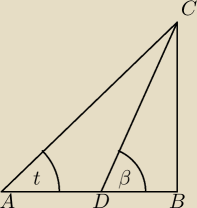
Zadanie z dwusieczną Mariusz: Jakiś czas temu dałem takie zadanie z dwusieczną Dane Przypadek I CB = x AB = a Przypadek II AC = x AB = a Przypadek III CB = x AC = a

	π
CD dwusieczna kąta		−t
	2

Obliczyć

CB
BD

dla każdego z trzech przypadków Teraz nie mogę tego wątku wyszukać Wynik wygląda dość ciekawie

Adamm:

	1+tg(t/2)
CB/BD=tgβ=tg(π/4+t/2)=		=
	1−tg(t/2)

	1+cost+sint
=		− to już jest proste do zapisania za pomocą a, x
	1+cost−sint

Mariusz: Z tego co pamiętam to Mila zaproponowała twierdzenie https://matematykaszkolna.pl/strona/498.html ale ja nie pamiętam abym miał je na lekcji a Jakub nie wykazał poprawności tego twierdzenia Poprawność tego twierdzenia można wykazać korzystając z a) podobieństwa trójkątów b) twierdzenia Talesa c) twierdzenia sinusów Twierdzenie Talesa i podobieństwo trójkątów miałem jeszcze w podstawówce a twierdzenie sinusów w liceum Długość trzeciego boku w trójkącie ABC obliczamy z twierdzenia Pitagorasa Na upartego można by to zadanko rozwiązać korzystając tylko z podobieństwa trójkątów Dlaczego uznałem że wynik wygląda dość ciekawie ? Uznałem tak ponieważ pozwoli nam wymyślić podstawienie które usunie niewymierność z całek postaci ∫R(x,√ax²+bx+c)dx