Ktoś: Mam pytanie: dlaczego szukajac minimum i maksimum funkcji

	1		1		1
P(x)=−		x3+		x2−		x+2 , gdzie x∊<0,2> sprawdzamy rowniez punkt x=0 skoro
	8		2		2

	2
P'(x)<0 dla x∊(−∞,		) wiec 0 miesci sie w tym przedziale?
	3

PW: Funkcja P jest badana na przedziale <0, 2>. Po co więc mówisz o jej pochodnej na przedziale

	2
(−∞,		)?
	3

Należy uznać, że funkcja P istnieje tylko na przedziale <0, 2>. Może ona osiagać ekstrema na krańcach dziedziny, i to trzeba sprawdzić osobno. Twierdzenie o ekstremum funkcji różniczkowalnej jest sformułowane dla przedziału otwartego.

Ktoś: tylko ze wtedy skad mam miec pewnosc ze jest to ekstremum, bo wiem ze po prawej stronie od zera funkcja jest rosnaca, ale nie wiem co sie dzieje po lewej stronie

piotr: Sprawdzamy punkty x∊<0,2>, w których f(x)=0 (o ile takie istnieją) oraz na końcach przedziału <0; 2>

piotr: ***w których f'(x)=0

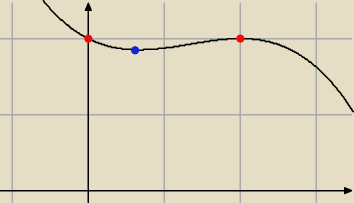
piotr: P(0)=2 → max P(2/3)=50/27 → min P(2)=2 → max

Ktoś: ok, dzieki