trójkąt Kasia: W trójkącie ABC: |AC|=b, |AB|=c i |∡BAC|=α poprowadzono dwusieczną kąta BAC,która przecięła bok BC w punkcie D wiedząc,że |AD|=d

	α		d(b+c)
wykaż,że cos		=
	2		2bc

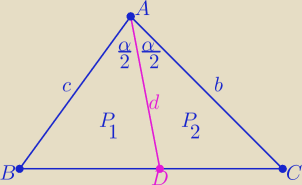
Eta: 1/ przejrzysty rysunek zgodny z treścią zadania

	1
2/ P(ABC)=		bc*sinα
	2

	1		1
P1=		dc*sin(α/2) i P2=		db*sin(α/2)
	2		2

P(ABC)=P₁+P₂ i sinα= 2sin(α/2)*cos(α/2) zatem 2bcsin(α/2)cos(α/2)= d(b+c)sin(α/2)

	d(b+c)
cos(α/2)=
	2bc

======================= c.n.w.