Narysować na płaszczyźnie zespolonej zbiory spełniające następujące warunki. mistrzuniobartex: 1) |z−2−i|=2|z+1−i| Odp. (x+2)²+(y−1)²=4 2) |z|+ re z<1 odp. x=<0,5 i y²<1−2x 3) |z−1|=|z−(−1+i)| odp. y=2x+0,5 Bardziej niż o rysunku( chociaż nimi tez nie pogardzę) prosiłbym jak to rozpisywać aby dostać się do tych odpowiedzi.

mistrzuniobartex: Poproszę o jakieś wskazówki.

Basia: ad.1 z = x+y*i |z−2−i| = |x+y*i−2−i| = |(x−2)+(y−1)*i| = √(x−2)²+(y−1)² |z+1−i| = |x+y*i+1−i| = |(x+1)+(y−1)*i| = √(x+1)²+(y−1)² i masz √(x−2)²+(y−1)² = 2√(x+1)²+(y−1)² /()² (x−2)²+(y−1)² = 4(x+1)² + 4(y−1)² x²−4x+4 + y²−2y+1 = 4x²+8x+4+4y²−8y+4 3x²+12x+3y²−6y +3 = 0 /:3 x²+4x+y²−2y+1 = 0 (x+2)²−4+(y−1)²−1+1=0 (x+2)²+(y−1)² = 4 okrąg S(−2;1) r=2 pozostałe podobnie

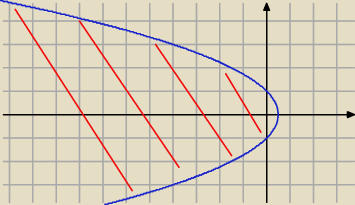
Basia: ad.2 z = x+y*i |z|+re(z) = √x²+y²+x czyli √x²+y²+x < 1 √x²+y² < 1−x a ta nierówność ma rozwiązanie ⇔

⎧	1−x>0
⎩	x2+y2 < (1−x)2

⎧	x<1
⎩	x2+y2 < 1−2x+x2

⎧	x<1
⎩	y2<1−2x

druga nierówność ma rozwiązanie ⇔ 1−2x>0 ⇔ 1>2x ⇔ x<0,5 ostatecznie mamy

⎧	x<0,5
⎩	y2<1−2x

rusujemy wykres funkcji y = √1−2x i wykres funkcji y= −√1−2x zaznaczamy czerwony obszar

Basia: trzecie jest łatwe; spróbuj sam

mistrzuniobartex: Dzięki. Już widzę o co chodzi.