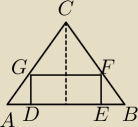
 Dany jest trójkąt równoramienny ABC o podstawie AB długości 6 i ramionach AC i BC takich, że
|AC|=|BC|=5. Rozważamy wszystkie prostokąty DEFG wpisane w trójkąt ABC w taki sposób,że na
ramieniu AC wybrano punkt G, a na ramieniu BC punkt F tak by bok GF był równoległy do podstawy
danego trójkąta oraz by bok DE prostokąta był zawarty w podstawie tego trójkąta.
Oblicz długości boków tego prostokąta DEFG, którego pole jest największe.
Pomóżcie proszę ! Doszedłem jedynie do wyznaczenia wzoru na długości boków mniejszych
prostokątów,z których
jest zbudowany ten duży prostokąt (3−x) i (4−y).
Dany jest trójkąt równoramienny ABC o podstawie AB długości 6 i ramionach AC i BC takich, że
|AC|=|BC|=5. Rozważamy wszystkie prostokąty DEFG wpisane w trójkąt ABC w taki sposób,że na
ramieniu AC wybrano punkt G, a na ramieniu BC punkt F tak by bok GF był równoległy do podstawy
danego trójkąta oraz by bok DE prostokąta był zawarty w podstawie tego trójkąta.
Oblicz długości boków tego prostokąta DEFG, którego pole jest największe.
Pomóżcie proszę ! Doszedłem jedynie do wyznaczenia wzoru na długości boków mniejszych
prostokątów,z których
jest zbudowany ten duży prostokąt (3−x) i (4−y).
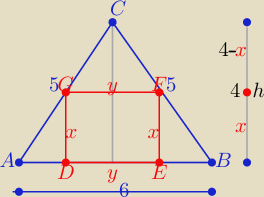 1/ h=4
z podobieństwa trójkątów ABC i FGC z cechy (kkk)
1/ h=4
z podobieństwa trójkątów ABC i FGC z cechy (kkk)
| 6 | 4 | ||
= | ⇒ y=6−1,5x , x∊(0,4) | ||
| y | 4−x |
| −6 | ||
dla odciętej wierzchołka czyli dla xmax= | = 2 to ymax=6−3=3 | |
| −3 |