Geometria analityczna- okręgi
Gejsza: Wyznacz równanie okręgu stycznego wewnętrznie do okręgu o równaniu (x − 2)2 + y2 = 4 i do
prostej y = 0 , którego środek ma współrzędne różnych znaków i leży na wykresie funkcji y=−x3
+ 1/4 .
6 kwi 19:36
Tadeusz:
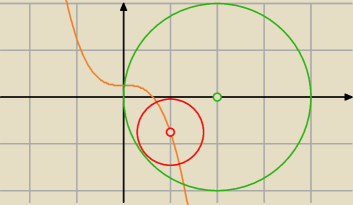
6 kwi 20:08
Gejsza: a jak obliczyć?
6 kwi 21:27
piotr: Szkic rozwiązania:
Układ równań z parametrem x0 ma mieć jedno rozwiązanie
(x−2)2 + y2 = 4
(x−x0)2 + (y+x03−1/4)2 = 0
⇒
Δ=4 − 4 x0 − 63 x02 + 64 x03 − 20 x04 + 4 x05 + 63 x06 − 64 x07 +
16 x08
Δ=0
⇒
x0 = −1, x0 = −(1/4), x0 = 1/4, x0 = 1, x0=2
x0 = 1/4 odpada
⇒
(1 + x)2 + (−(5/4) + y)2 = 25/16,
(1/4 + x)2 + (−(17/64) + y)2 = 289/4096,
(−(1/4) + x)2 + (−(15/64) + y)2 = 225/4096, odpada
(−1 + x)2 + (3/4 + y)2 = 9/16,
(−2 + x)2 + (31/4 + y)2 = 961/16,
6 kwi 22:14
piotr: x0 = 2 też należy odrzucić, wynika to z rozwiązania układu względem x0
czyli odpada równanie:
(−2+x)2+(31/4+y)2=961/16
6 kwi 22:54
piotr:
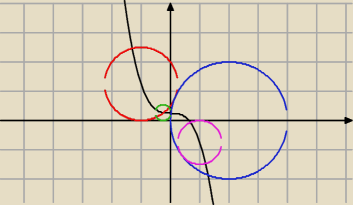
7 kwi 00:21
aniabb: Piotr czemu w drugim równaniu masz =0


7 kwi 06:27
aniabb:
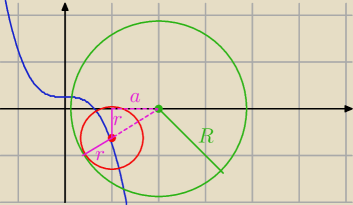
a może tak?
mały okrąg jest styczny do y=0 więc r=y
0
Pitagoras
a
2+r
2=(R−r)
2
(2−x
0)
2+(y
0)
2 = (2−|y
0|)
2
I przypadek
(2−x)
2+(−x
3+1/4)
2=(2+x
3−1/4)
2
−4x
3+x
2−4x+1=0
x=1/4
y=15/64
te same znaki
II przypadek
(2−x)
2+(−x
3+1/4)
2=(2−x
3+1/4)
2
4x
3+x
2−4x−1=0
x=1
y=−3/4
7 kwi 06:41
aniabb: x=−1 i −1/4 nie spełniało założenia, że styczne wewnętrznie
7 kwi 06:58
piotr: **pomyłka, ma być:
(x−x0)2 + (y+x03−1/4)2 = (x03−1/4)2
obliczenia poprawne
7 kwi 15:55




 a może tak?
mały okrąg jest styczny do y=0 więc r=y0
Pitagoras
a2+r2=(R−r)2
(2−x0)2+(y0)2 = (2−|y0|)2
I przypadek
(2−x)2+(−x3+1/4)2=(2+x3−1/4)2
−4x3+x2−4x+1=0
x=1/4
y=15/64
te same znaki
II przypadek
(2−x)2+(−x3+1/4)2=(2−x3+1/4)2
4x3+x2−4x−1=0
x=1
y=−3/4
a może tak?
mały okrąg jest styczny do y=0 więc r=y0
Pitagoras
a2+r2=(R−r)2
(2−x0)2+(y0)2 = (2−|y0|)2
I przypadek
(2−x)2+(−x3+1/4)2=(2+x3−1/4)2
−4x3+x2−4x+1=0
x=1/4
y=15/64
te same znaki
II przypadek
(2−x)2+(−x3+1/4)2=(2−x3+1/4)2
4x3+x2−4x−1=0
x=1
y=−3/4