stereometria aksjomat matmajestsuper: W sześcian wpisano kulę, w którą wpisany jest drugi sześcian. Oblicz stosunek objętości sześcianu większego do objętości sześcianu mniejszego. W odpowiedziach jest 3√3, a mi wychodzi 2√2, wkradł się błąd w książce czy coś przeoczyłam? V_{wiekszego szescianu} = a³ V_kuli = ⁴₃ * π * (^a₂)³ V_{mniejszego szescianu} = (^a*√2₂)³ stosunek = ^a3_a³*2*√2 * 8 = 2* √2

Adamm: w odpowiedzi jest poprawnie 1. objętość kuli policzona niepotrzebnie 2. objętość mniejszego sześcianu jest równa (a/√3)³

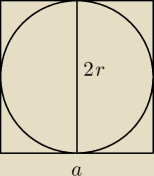
matmajestsuper: czemu objętość kuli jest policzona nieprawidłowo? bok sześcianu jest równy a, a więc promień jest równy ^a₂

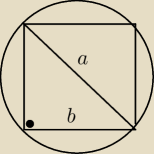
matmajestsuper: i skoro średnica kuli jest równa a, a wpisujemy do niej sześcian, to a = b√3 czyli b= ^a*√2₂

matmajestsuper: *edit, przeczytałam nieprawidłowo,zamiast niepotrzebnie

Eta: Duży sześcian o krawędzi a=2R ma objętość V₁=8R³ mały sześcian o krawędzi b gdzie b√3=2R ⇒ b=2R/√3 ma objętość V₂=8R³/3√3 to V₁/V₂= 3√3 ===========

matmajestsuper: dziękuję za rozwiązanie ale czemu b√3=2R ⇒ b=2R/√3? nie powinno być b√2=2R ⇒ b=2R/√2? (zrobiłam błąd o 1:26)

matmajestsuper: bierzemy przekątną sześcianu zamiast jego podstawy?

matmajestsuper: już rozumiem, dzięki za pomoc