ostrosłup ścięty szymczyk: Niech ABCD i A₁B₁C₁D₁ będą podstawami prawidłowego ostrosłupa ściętego ABCDA₁B₁C₁D₁ (podstawy są kwadratami i są równolegle rys.poniżej ). Przez przekątną AC₁ bryły przechodzi płaszczyzna k równoległa do przekątnej BD podstawy ABCD. Oblicz stosunek objętości brył orzymanych w wyniku podziału płaszczyzną k, jeśli AC = 6 i A₁C₁ = 2. https://commons.wikimedia.org/wiki/Category:Frustums_of_4-gon_pyramids#/media/File:Usech_kvadrat_piramid.png Czy to jest możliwe ja nawet nie mogę sobie wyobrazić jak by ta płaszczyzna była ułozona

szymczyk: Czy ktoś może mi wyjaśnić chociaż na rysunku jak to ma wyglądac

szymczyk: nikt nie umie

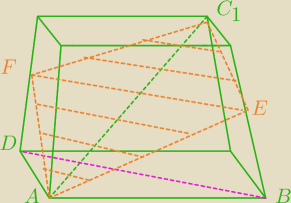
iteRacj@: |DF|=|EB| po narysowaniu w Geogebrze widać że to deltoid (tutaj niestety nie widać)

szymczyk: A mozesz dac link do gegogebry?

iteRacj@: mogę tylko wstawić obrazek https://zapodaj.net/488fd4e06f62f.png.html

szymczyk: Dziekuje a nie mozesz zamieścić gdzieś pliku, bo na tym rysunku tez jest dla mnie nie jasne

iteRacj@: próbuję wysłać i zgłasza mi błąd

szymczyk: a mozesz jako aplet na stronie geogebry lub tu https://megawrzuta.pl/

iteRacj@: tutaj jest animacja https://zapodaj.net/2ac32d3eb5e0c.gif.html

iteRacj@: plik ggb https://megawrzuta.pl/download/5c27df76eccb1b2e24ed38ad3b99ec57.html

szymczyk: w końcu jakoś to widzę Wiem jaki jest wzór na objetość ostrosłupa ściętego, ale jak sobie poradzić teraz z tymi objetosciami?

Mila: Iteracjo

iteRacj@: @Milu podziękowania należą się twórcom Geogebry. Stworzyli świetne, dostępne dla każdego narzędzie, dzięki któremu o wiele łatwiej i szybciej można się uczyć. Kto jeszcze nie ma Geogebry, niech od razu zacznie korzystać.

szymczyk: Dzieki a jak go rozwiązać?