funkcja liniowa z parametrem Qba: Dla jakich wartosci m proste o rownaniach y=2mx+1 i y=mx+m przetną się w punkcue (x,y), którego obie współrzędne będą tego samego znaku? Pomoże ktoś zacząć?

uki: wyznacz x i y z układu a potem x*y>0

Qba: okej wyznaczylem, a jak teraz znalezc punkt?

Qba: dotarłem do czegos takiego: yx+y−x−1>0 (z tego warunku x*y>0) nie mam pomysłu co teraz, pomoże ktoś?

Eta: y=2mx+1 i y=mx+m to:

	m−1
2mx+1=mx+m ⇒ mx=m−1 ⇒ x=		, m≠0
	m

==========

	m−1
y= m*		+m ⇒ y= 2m−1
	m

==========

	m−1
x*y>0 ⇒		*(2m−1)>0 /*m2
	m

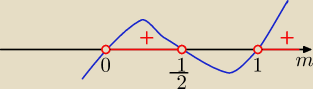
m(m−1)(2m−1)>0 m∊(0,1/2)U(1,∞) ==============

Eta: I co Qba? .... przepisałeś gotowca? i masz to w......................................

Qba: Nie Eta, przepraszam ale musialem gdzies wyjsc, dziekuje za pomoc

Eta: