Długości krawędzi podstawy prostopadłościanu są równe 3cm,4cm. Krawędź boczna ma RiviT: Długości krawędzi podstawy prostopadłościanu są równe 3cm,4cm. Krawędź boczna ma długość 2cm. Oblicz pole przekroju tego graniastosłupa płaszczyzną zawierającą przekątną podstawy i nachyloną do płaszczyzny podstawy pod kątem 60 stopni

aniabb: 5•2,4=12

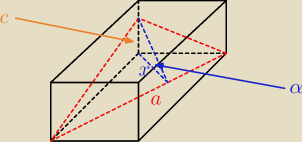
Blee: α = 60^o 1) obliczamy 'x' (wysokość trójkąta będącego połową podstawy) P_p = 3*4 = 12

Pp		a*x		12
	= 6 = Pp Δ =		−> a*x = 12 −> x =		= 2.4
2		2		5

2) wyliczamy wysokość przekroju:

	x		1		2.4
cos60o =		−>		=		−> h = 4.8
	h		2		h

3) (WAŻNE) sprawdzamy czy przekrój wygląda na pewno tak jak na rysunku (czy przekrojem przypadkiem nie będzie trapez. W tym celu sprawdzamy, czy c<2

	c		√3		c
cos60o =		→		=		−> c = 2.4*√3 > 2
	h		2		4.8

Wniosek ... to rozwiązanie jest błędne ... trzeba zacząć od początku, tym razem wiedząc, że przekrojem będzie trapez

Blee: Aniu −−− Ty policzyłaś połowę pola podstawy

aniabb: nie sprawdziłam czy nie za niski policzyłam 5•4,8/2 czyli pole trójkąta

aniabb: no to skoro trapez to a=5 b=25√3/18 h=4√3/3 no i pole =(a+b)•h/2

RiviT: A jak sprawdzić czy za niski czy za wysoki

Blee: Napisałem przecież −−− punkt (3) się kłania ... nawet napisałem WAŻNE

RiviT: A jak policzyć długość krótszej podstawy? aniabb napisała wymiary ale nie wiem jak to obliczyć

aniabb: z proporcji

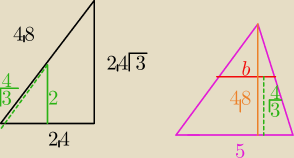
aniabb: i znów było nie w tę stronę ...za dużo próbuję w pamięci

b		4,8−4/√3
	=
5		4,8

aniabb: b=5−25√3/18