Twierdzenia cosinusow Gość : W trójkącie boki mają długość a, b, c, natomiast miary kątów są odpowiednio równe alfa, beta, gamma. Wykaż, że jeśli a×cosbeta=b×cosalfa, to trójkąt ten jest równoramienny.

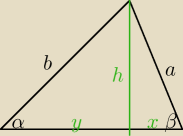
aniabb: a•cosβ = b•cosα

	x		y
a•		b•
	a		b

x=y skoro x=y h=h to a=b (z piagorasa)

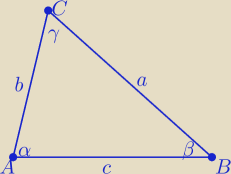
Eta: Z tw. cosinusów

	c2+a2−b2		b2+c2−a2
cosβ=		i cosα=
	2ac		2bc

	c2+a2−b2		b2+c2−a2
to a*cosβ= b*cosα ⇒		=		⇒ ... 2a2=2b2 ⇒ a=b
	2c		2c

więc trójkąt jest równoramienny