Pochodna Weronika: Jaka powinna być długość podstawy AB trapezu ABCD, aby jego pole było największe, jeśli długość każdego z pozostałych boków tego trapezu jest równa 10? Oblicz to pole. Doszłam do momentu gdzie P(x) = ¹₄ * √{10+x}²*√−x²+20x+300 i nie wiem jak obliczyć z tego pochodną.

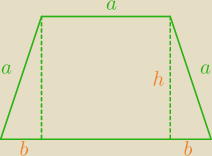
iteRacj@: rozwiązałam po swojemu, bo nie wiem co u Ciebie oznacza x a=10, 0<b<10

	2a+2b
P=h		=h(10+b)
	2

h²=a²−b², h²=100−b² P(b)=(10+b)√100−b² = √(100−b²)(10+b)²= √(100−b²)(100+20b+b²)= =√(100−b²)(100+20b+b²)=√−b⁴−20b³+2000b+10000 pole trapezu będzie największe, gdy wartość funkcji pod pierwiastkiem będzie największa oblicz pochodną funkcji pod pierwiastkiem i znajdź jej miejsca zerowe, sprawdź, czy jest wśród nich maksimum spełniające warunek 0<b<10 oblicz dłuższą podstawę

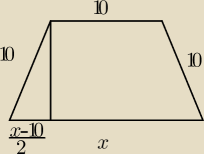
Weronika: Ja zrobiłam w ten sposobów i właśnie utknęłam bo nie mam pojęcia jak z takiej pochodnej przejść dalej. Wiem tylko, że powinno wyjść f'(x) = −4x³ +1200x + 8000 ale nie umiem do tego dojść Twój sposób też jest dobry, wielkie dzięki!

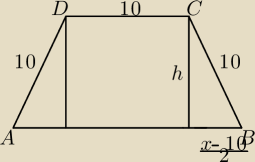
jackie chan: |AB| = x, zalozenie: x>0

	h
P = (10+x)*
	2

	x−10
zalozenie:		> 0 −−> x>10
	2

	x−10		(x2−20x+100)		−x2+20x+300
h2=100−(		)2 = 100 −		=
	2		4		4

	√−x2+20x+300
h =
	2

zalozenie: −x²+20x+300 > 0 Δ_x = 400 + 4*1*300 = 1600 −−> √Δ_x = 40

	−20−40
x1 =		= 30
	−2

	−20+40
x2 =		= −10
	−2

(x−30)(x+10) > 0 −−−> x>30 (bo x>10 z wczesniejszego zalozenia)

	1
P(x) =		(10+x)*√−x2+20x+300
	4

wlaczmy (10+x) pod pierwiastek

	1
P(x) =		√(10+x)2*√−x2+20x+300
	4

teraz 2 sposoby 1) Niech funkcja f(x) = (10+x)²*√−x²+20x+300 przyjmuje ona maksimum dla tego samego argumentu co P(x) tylko inna wartosc, zatem znajdujemy maksimum f(x) i dla tego argumentu liczymy wartosc P(x) 2) Liczymy pochodna zlozona:

	1		1
P'(x) =		*[		* [(10+x)2*√−x2+20x+300]' ]
	4		√(10+x)2*√−x2+20x+300

i wtedy oczywiscie gdy P'(x) = 0 to to wszystko z pierwiastkiem znika i i tak zostaje tylko pochodna [(10+x)²*√−x²+20x+300]'

jackie chan: tego drugiego pierwiastka nie powinno byc oczywiscie jak jest √(10+x)² * (−x²+20x+300) <−− bo to (10+x)² jest pod tym samym pierwiastkiem

Weronika: już rozumiem, teraz wszystko ładnie wyszło, dzięki wielkie!