Trójkąty
Pingwin4: Dany jest trójkąt równoramienny abc o podstawie ab równej 6 i ramionach rownych 5. Rozważmy
wszystkie prostokąty defg wpisane w trójkąt abc w taki sposób, że na ramieniu ac wybrano punkt
g a na bc punkt f tak by bok gf był równoległy do podstawy dnego trójkąta obraz by bok de
prostokąta byl zawarty w podstawie. Oblocz długości bokow prostkata którego pole jest
największe.
4 kwi 17:43
Pingwin4: Zadanie jest z funkcją wymierną
4 kwi 17:57
piotr:
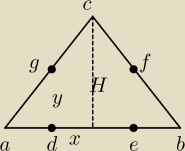
H=4
P=2*x*y
4/3 = y/(3−x)
P(x)=8x(3−x)/3
P'(x)=8 − (16 x)/3
P'(x)=0 ⇒ x =3/2
P
max(3/2) = 6
|de| = 2x = 3
|dg = |y = 2
4 kwi 18:00
Pingwin4: Jeszcze raz dziękuję

4 kwi 18:04
Blee:
Odpowiedni rysunek wymagany
Oznaczmy dlugosci bokow prostokata jako 2x i 2y gdzie 2x jest rownolegly do podstawy.
Zauwazamy podobienstwo trojkatow prostokatnych:
Gdzie h=4
Stad masz proporcje pomiędzy bokami.
Tworzysz rownanie kwadratowe i wyliczasz wspolrzedne wierzchołka paraboli
4 kwi 18:05
 H=4
P=2*x*y
4/3 = y/(3−x)
P(x)=8x(3−x)/3
P'(x)=8 − (16 x)/3
P'(x)=0 ⇒ x =3/2
Pmax(3/2) = 6
|de| = 2x = 3
|dg = |y = 2
H=4
P=2*x*y
4/3 = y/(3−x)
P(x)=8x(3−x)/3
P'(x)=8 − (16 x)/3
P'(x)=0 ⇒ x =3/2
Pmax(3/2) = 6
|de| = 2x = 3
|dg = |y = 2
