Dany jest trójkąt ABC Ktoś: Dany jest trójkąt ABC taki, że AC=2AB. Miara kąta ACB jest o 30 stopni mniejsza od miary kąta ABC. Oblicz tangens kąta ACB. To zadanko juz pojawilo sie na tym forum ale nie rozumiem jednej rzeczy: 2sinα= sin(α+30) 2sinα=sinα*cos30+cosα*sin30 (4−√3)sinα=cosα nie wiem jak z tego obliczyc tg, poniewaz teoretycznie powinno sie chyba podzieli przez cos i

	1
wtedy wychodzi, ze tgα=		ale cosα moze byc chyba zerem a wtedy nie mozna dzielic
	4−√3

jackie chan: sprawdz co sie dzieje po prostu dla cosα = 0

	π
czyli cosα = 0 dla α =		+ kπ
	2

to podstawmy do tego rownania

	π
(4−√3)sinα = cosα za alfe
	2

(4−√3) * 1 = 0 4−√3 = 0 sprzecznosc, zatem cosinus nie moze byc zerem. wiec mozesz podzielic

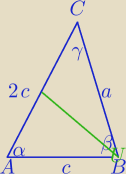
Mila: β=γ+30

1		1
	*2c*a*sinγ=		*c*asinβ − porównanie pól
2		2

2sinγ=sin(γ+30)

	√3		1
2sinγ=		sinγ+		cosγ
	2		2

cosγ=(4−√3) sinγ cosγ≠0 , |bo AB|=c<|AC|=2c

	1
tgγ=
	4−√3