Wyjaśni ktos jak się robi takie zadania? 😥😭 Kasia: Dany jest kwadrat ABCD O wierzcholkach A=(−8,3)B=(−5,2)C=(−4,5)D=(−7,6). Obraz jednego z tych wierzchołków w jednokladnosci o środku w punkcie A i skali ujemnej leży na prostej l o rownaniu x−2y−6=0. Wyznacz współrzędne wierzchołków obrazu kwadratu ABCD w tej jednokladnosci.

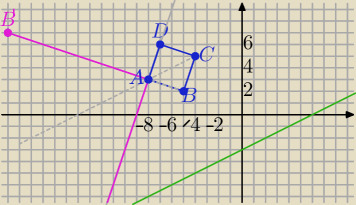
Mila: A=(−8,3)B=(−5,2)C=(−4,5)D=(−7,6). |AD|=√1²+3²=√10 A'=A(−8,3) AD'^→=k*AD^→ 1) Prosta AD: AD^→=[1,3]

x+8		y−3
	=
1		3

y=3x+27 D'− Punkt przecięcia prostych y=3x+27 i x−2y−6=0 x=−12 i y=−9 D'=(−12,−9) 2) ustalenie skali, k<0 A(−8,3) AD'^→[−4,−12], |AD'|=√4²+12²=4√10 k=−4 3)C', AC^→=[4,2] AC'^→[x+8,y−3]=−4*[4,2]⇔x=−24,y=−5 C'(−24,−5) 4)B=(−5,2), B' AB^→[3,−1] AB'^→[x+8,y−3]=−4*[3,−1] x+8=−12, y−3=4 x=−20, y=7 B'=(−20,7) =============