Ekstremum
Studentka: Wyznaczyć ekstrema lokalne podanych funkcji:
f(x)=|x2−1|
2 kwi 19:49
Studentka: Mam pytanie czy funkcja w punktach −1 lub 1 posiada ekstremum? Czego np funkcja |x| nie posiada
ekstrmum w pkt 0
2 kwi 20:20
Mila:
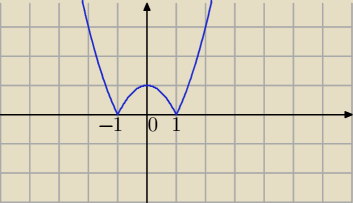
f(x)=|x
2−1|
Ekstrema lokalne :
w x=−1, x=1, x=0
Natomiast w x=(−1) , x=1 funkcja f(x) nie posiada pochodnej.
2)
g(x) =|x| ma minimum w x=0, nie ma pochodnej w x=0
2 kwi 20:24
Mila:
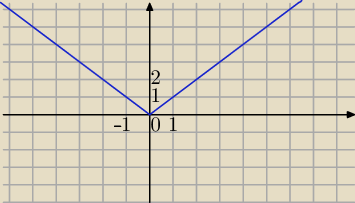
g(x)=|x|
2 kwi 20:25
Studentka: Jak wykazać, że funkcja f (x) nie posiada pochodnej w pktcie −1 lub 1 ?
Przeciez f (x) jest ciągła w tych punktach.
2 kwi 20:33
Studentka: A f− ' (1) = f+ ' (1)
2 kwi 20:35
Studentka: Chyba ze coś źle licze
2 kwi 20:36
Studentka: | | f(Δx+1)−f(1) | | |Δx2+2Δx| | |
f−'(1)=lim(Δx−>1−)( |
| )=lim(Δx−>1−)( |
| )=Δx+2=3 |
| | Δx | | Δx | |
f
+'(1)=Δx+2=3
2 kwi 21:04
Mila:
f(x)=|x
2−1|
x=1
| | f(1+h)−f(1) | | |(1+h)2−1|−|1−1| | |
limh→0− |
| =limh→0− |
| = |
| | h | | h | |
| | |h|*|(2+h)| | |
=limh→0− |
| =−1*2=−2 |
| | h | |
| | f(1+h)−f(1) | | |(1+h)2−1|−|1−1| | |
limh→0+ |
| =limh→0+ |
| = |
| | h | | h | |
| | |1+2h+h2−1| | | h*(2+h) | |
=limh→0+ |
| =limh→0+ |
| =1*2=2 |
| | h | | h | |
2 kwi 21:53
 f(x)=|x2−1|
Ekstrema lokalne :
w x=−1, x=1, x=0
Natomiast w x=(−1) , x=1 funkcja f(x) nie posiada pochodnej.
2)
g(x) =|x| ma minimum w x=0, nie ma pochodnej w x=0
f(x)=|x2−1|
Ekstrema lokalne :
w x=−1, x=1, x=0
Natomiast w x=(−1) , x=1 funkcja f(x) nie posiada pochodnej.
2)
g(x) =|x| ma minimum w x=0, nie ma pochodnej w x=0
 g(x)=|x|
g(x)=|x|