optymalizacja nie zdam matury: Znajdź współrzędne takiego punktu A leżącego na paraboli o równaniu y=−x2 +4x , aby styczna do tej paraboli poprowadzona z punktu A wraz z prostymi x = 0, x = 2, y − 0 wyznaczały trapez o możliwie najmniejszym polu. Nie umiem znalezc rozwiazania tego zadania nigdzie

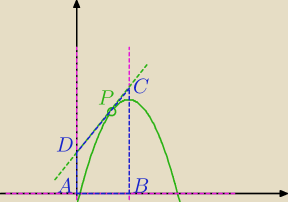
iteRacj@: najpierw ustal puknty wspólne wykresu paraboli z osią OX, przyjminj P=(x_o, −x_o²+4x_o) P_ABCD=1/2*(|AD|+|BC|)*|AB| skorzystaj ze wzoru na równanie stycznej do krzywej w danym punkcie jak będziesz znać wzór tej stycznej czyli prostej AC znajdź wspłórzędne pktów A i C oblicz |AD| i |BC| otrzymasz wzór na pole trapezu policz pochodną i znajdź minimum

iteRacj@: * poprawka: czyli prostej DC znajdź współrzędne punktów D i C