Oblicz długość przekątnej i powierzchni ściany bocznej tego graniastosłupa
Natalia333: Przekątne graniastosłupa prawidłowego sześciokątnego mają długość
6√3 i 3√13.
Oblicz : a) długość przekątnej ściany bocznej graniastosłupa,
b) pole powierzchni bocznej tego graniastosłupa.
Obliczyłam, że bok podstawy = 15
Nie wiem co dalej.. Pomocy !
2 kwi 16:09
pomoc drogowa: A mi wyszło a = 3 .... na pewno 15

2 kwi 16:45
Natalia333: Hym... mi wychodzi 15... a możesz napisać obliczenia?
2 kwi 16:51
pomoc drogowa:
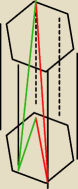
Rysunek trochę tragiczny, ale nie chodzi o to:
czerwona linia − długość przekątnej 3
√13 oraz długość podstawy 2a (2 razy długość podstawy
trójkąta równobocznego a)
zielona linia − długość przekątnej 6
√3 oraz długość podstawy a
√3 (2 razy wysokość trójkąta
Tw. pitagorasa:
(3
√13)
2 = H
2 + (2a)
2
(6
√3)
2 = H
2 + (a
√3)
2
gdzie H − wysokość graniastosłupa
z tego wyliczamy a
Następnie należy wyliczyć wysokość H i znowu z tw. pitagorasa obliczyć długość przekątnej
ściany bocznej (oznaczmy ją jako x)
x
2 = H
2 + a
2 (mi wyszło 3
√10)
Na koniec należy obliczyć punkt b (zostawiam już to Tobie samej, mi wyszło 162 [j
2])
2 kwi 17:01
Natalia333: Dzięki

2 kwi 17:15
Krzysiek60:
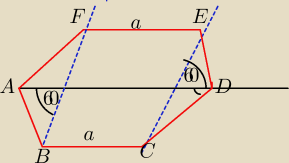
to jest rzut rownolegly szesciokata
AD − przekatna
a bok
ABIIED
AFIICD
Zobacz z e przy takim rzucie wierzcholki Ci sie nie pokryja
2 kwi 19:11

 Rysunek trochę tragiczny, ale nie chodzi o to:
czerwona linia − długość przekątnej 3√13 oraz długość podstawy 2a (2 razy długość podstawy
trójkąta równobocznego a)
zielona linia − długość przekątnej 6√3 oraz długość podstawy a√3 (2 razy wysokość trójkąta
Rysunek trochę tragiczny, ale nie chodzi o to:
czerwona linia − długość przekątnej 3√13 oraz długość podstawy 2a (2 razy długość podstawy
trójkąta równobocznego a)
zielona linia − długość przekątnej 6√3 oraz długość podstawy a√3 (2 razy wysokość trójkąta

 to jest rzut rownolegly szesciokata
AD − przekatna
a bok
ABIIED
AFIICD
Zobacz z e przy takim rzucie wierzcholki Ci sie nie pokryja
to jest rzut rownolegly szesciokata
AD − przekatna
a bok
ABIIED
AFIICD
Zobacz z e przy takim rzucie wierzcholki Ci sie nie pokryja