Bryły Agata: Czołem Naszło mnie na zadania W ostrosłupie prawidłowym trójkątnym wysokosc bryły jest dwa razy większa od krawedzi podstawy , a promien okregu wpisanego w podstawe bryły ma 3√3 . Olicz objętość ostrosłupa i pole powierzchni bocznej.

Jack: V = 3 P_b = 43

Jack: prima aprilis

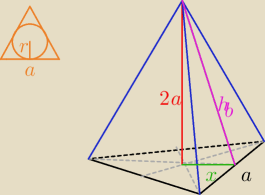Jack: ten maly rys. po lewej u gory to podstawa tego ostroslupa skoro promien r = 3√3 to wysokosc trojkata wynosi 3r = 9√3 zatem znajdzmy 'a':

	a√3
h =
	2

	a√3
9√3 =
	2

18√3 = a√3 a = 18 zatem wysokosc calego ostroslupa: H = 2*18 = 36. Zatem objetosc

	1		a2√3
V =		*		* H = ...
	3		4

	1
Fragment zielony − x wynosi		* h = 3√3
	3

z pitagorasa wiec obliczamy h_b − wysokosc boczna i wtedy

	1
Pb = 4*(		* a * hb) <−− 4 takie trojkaty
	2

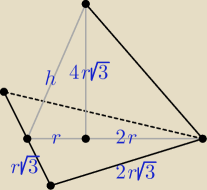Bogdan: Można oznaczyć długości tak, aby obliczenia były prostsze, skróci się wtedy czas rozwiązywania zadania. h = √ 48r² + r² = 7r