Maksymalny przedział na którym funkcja f(x)=mx^3+mx^2-8x-9 jest malejąca ma dług maturzysta: Maksymalny przedział na którym funkcja f(x)=mx³+mx²−8x−9 jest malejąca ma długość 2. Oblicz wartość parametru m oraz wyznacz największą wartość funkcji w przedziale <−2 1>. Proszę o pomoc w ciekawym zadanku, z góry dzięki Nie wiem za bardzo jak wykorzystać informację, że długość tego przedziału wynosi 2

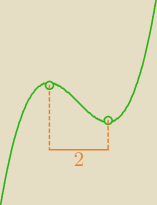
iteRacj@: 1/ wniosek: z tej informacji wynika, że funkcja jest wielomianem stopnia trzeciego i m>0, spójrz na rysunek 2/ wniosek: należy obliczyć pochodną funkcji, gdyż odległość między jest miejscami zerowymi będzie wynosić 2 |x₁−x₂|=2 to pozwoli wyznaczyć m

===: Funkcja malejąca w danym przedziale ... pochodna mniejsza od zera Licz pochodną i zastanów sie jak policzyć odległość między x₁ a x₂

maturzysta: Dzięki wielkie za pomoc, rozjaśniłeś mi umysł, chyba już wiem jak ale skończę jutro bo dziś już późno