zad QWERTY: Uzasadnij, że nie istnieją dwie liczby, których suma jest równa 10, a iloczyn jest większy od 25. czyli uklad rownan x+y=10 x*y>25 x=10−y 10−y²>25 y²−10y+25<0 Δ=100−100 Δ=0 y=5 czyli x=5 No i nie wiem

Krzysiek60: Nie zapisuj x*y>25 bo tego nie wiesz x+y=10 ⇒x= 10−y (10−y)y= 10y−y² funkcja 10y−y² osiaga maksimum w wierzcholku i to maksimun wynosi y=5 stad x=5 x*y=5*5=25 i wiekszse nie moze byc Mozesz sobie to sprzwdzic np x=2 y=8 iloczyn 16

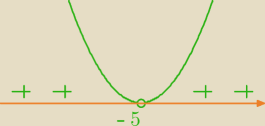
iteRacj@: y²−10y+25<0 (y−5)²<0 funkcja przyjmuje tylko wartości nieujemne! brak rozwiązań

iteRacj@: *na rysunku miało być 5