Trygonometryczne maturka: Jak w łatwy sposób wykazać że jeżeli sinx+siny=1 to √1+sin²x+√1+sin²y≥√5?

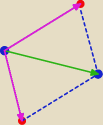
Adamm: a=sinx, b=siny a+b=1 √(a+b)²+a²+√(a+b)²+b²≥√((a+b)+(a+b))²+(a+b)² √1+sin²x+√1+sin²y≥√5 z nierówności Minkowskiego Inny sposób (choć praktycznie taki sam) geometrycznie (1, sinx) oraz (1, siny) suma ich odległości od (0, 0) jest większa (bądź równa) od (2, sinx+siny) żeby to zobaczyć, rysunek wektory (odcinki) różowe są > (ale tylko kiedy tworzą trójkąt, gdy tak nie jest mamy równość) od zielonej przekątnej

maturka: No ten z wktorami bardziej do mnie przemawia