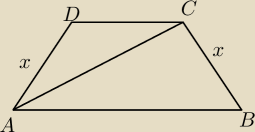
 Dany jest trapez równoramienny ABCD. Wykazać, że promień okręgu opisanego na trójkącie ABC jest
również promieniem okręgu opisanego na trapezie ABCD.
A TAK W OGÓLE TO WESOŁYCH ŚWIĄT MOI MILI
Dany jest trapez równoramienny ABCD. Wykazać, że promień okręgu opisanego na trójkącie ABC jest
również promieniem okręgu opisanego na trapezie ABCD.
A TAK W OGÓLE TO WESOŁYCH ŚWIĄT MOI MILI
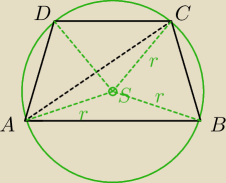 S środek okregu opisanego na ΔABC
|SB|=|SC|=|AC|=r
|<SAB=|<SBA| oraz |<DAB=|<CBA|
stąd |<DAS=|<CBS|
|<CDS=|<DCS| oraz |<ADC=|<DCB|
stąd |<ADS|=|<BCS|
oraz |<DSA|=|<CSB|
ΔADS≡ΔCBS (kbk) ⇒ |DS|=|CS|=r
Wesołych Świat również życzę!
S środek okregu opisanego na ΔABC
|SB|=|SC|=|AC|=r
|<SAB=|<SBA| oraz |<DAB=|<CBA|
stąd |<DAS=|<CBS|
|<CDS=|<DCS| oraz |<ADC=|<DCB|
stąd |<ADS|=|<BCS|
oraz |<DSA|=|<CSB|
ΔADS≡ΔCBS (kbk) ⇒ |DS|=|CS|=r
Wesołych Świat również życzę!
