arctgoo Miloszek11143: ile to jest arctg z nieskonczonosci?

Adamm: nie ma czegoś takiego

Jerzy:

	π
Natomiast ten arc zmierza do
	2

Miloszek11143: bo mam cos takiego korzystając z reguly de l'hospitala lim(π−2arctgx)lnx x→∞ to jak podstawiam za x ∞ to mi wychodzi wlasnie 2arctg∞ do obliczenia ktoś kuma jak sie zabrać za ten przykład?

Adamm: Jak masz x→∞ to nie podstawiaj tego pod funkcję. Jeśli podstawiasz jakąś LICZBĘ pod funkcję i wyjdzie ci coś normalnego, w porządku. Ale, to co teraz zrobiłeś to jest według mnie obraza dla sztuki jaką jest matematyka.

Miloszek11143: eTrapez tak uczy i jest wszystko ladnie

Miloszek11143: w takim razie pokaż mi jak prawidłowo obliczyć tę granicę

Miloszek11143: z resztą nie podstawiam do samego równania tylko tak nieformalnie liczę na boku w nawiasie kwadratowym

Adamm: jak będzie ci eTrapez kazał skakać z okna, to skoczysz?

Miloszek11143: weź się nie przypierdalaj jak nie chcesz pomóc, skądś się musze uczyć.

Mila: Oj, Miloszek, nieładnie

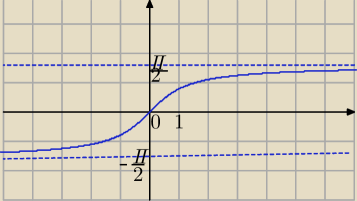
Mila: f(x)=arctg(x)

	π
limx→∞arctg(x)=
	2

Mila: Kolega Adam ma rację . Jeżeli napiszesz na kolokwium arctg(∞) to dostaniesz za całe zadanie zero punktów.

jc: To jeszcze jako skrót mógłbym zaakceptować. Ale lim_n→∞ 1/n = 1/∞ = 0 już nie.