Zadanie maturalne maturka: Dany jest ostroslup prawidłowy trójkątny. Z dowolnego punktu P jego podstawy prowadzimy prosta k prostopadła do podstawy. Udowodnij że suma długości odcinków łączących punkt P z punktami przecięcia prostej k ze ścianami bocznymi nie zależy od wyboru punktu P i jest równa trzykrotnej wysokości ostroslupa.

===: ... treść zadania

maturka: Co treść zadania?

===: to ile tych scian bocznych przecina prosta prostopadła do podstawy ostrosłupa

maturka: Wg mnie ze wszystkimi ścianami bocznymi, że tak wynika z treści. Tak jest treść zadania maturalnego że starej matury.

===: ... aż tak pijany nie jestem

maturka: O co chodzi?

Mila:

Mila: Napisz linka do tej matury

===: o dokładne przepisanie "przerysowanie" treści zadania

maturka: http://wstaw.org/m/2018/04/01/IMG_20180401_212952.jpg

maturka: Zdjęcie powyżej bo mam to na kartce

===: ... i co ... nie widzisz różnic w treści ... radosna twórczość

maturka: A jak jest różnica?

===: ... w rozmowie dziada z obrazem

maturka: Ok wiem już bo zabrakło płaszczyzny sorry

maturka: No ok a jak to rozwiązać w takim razie?

===: Przepisz tu słowo w słowo treść zadania. To co zamieszczasz czytelne nie jest ! Zgaduj zgadula to dwa pokoje dalej

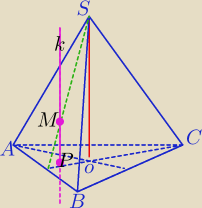
maturka: Dany jest ostroslup prawidłowy trójkątny. Z dowolnego punktu P jego podstawy prowadzimy prosta k prostopadła do płaszczyzny podstawy. Udowodnij że suma długości odcinków łączących punkt P z punktami przecięcia prostej k z płaszczyznami zawierającymi ściany boczne ostroslupa nie zależy od wyboru punktu P i jest równa trzykrotnej wysokości ostroslupa

maturka: Czy już czytelnie?

maturka: I?

===: Z punktu P poprowadź prostopadłe do poszczególnych krawędzi podstawy ostrosłupa. Powstałe odcinki oznacz jako h₁, h₂ i h₃

	a√3
Łatwo wykażesz, że h1+h2+h3=		gdzie a to bok podstawy
	2

Ściany boczne ostrosłupa nachylone są do płaszczyzny podstawy pod kątem α Odcinki łączące punkt P z punktami przecięcia prostej k ze ścianami bocznymi ozacz jako x, y, z Szukasz oczywiście x+y+z.

x
	=tgα ⇒ x=h1tgα
h1

y
	=tgα ⇒ y=h2tgα
h2

z
	=tgα ⇒ z=h3tgα
h3

	a√3
x+y+z=tgα(h1+h2+h3)=		*tgα
	2

Spodek wysokosci ostrosłupa dzieli wysokość podstawy w znanym Ci stosunku.

	H
Jeśli wysokosc ostrosłupa oznaczysz jako H to		=tgα
	1   a√3   * 3   2

	a√3
stąd H=		tgα
	6

Dla Ciebie pozostawiam porównanie x+y+z z H

maturka: Dziękuję no teraz to już łatwo widać tgα=H : 1/3h gdzie H to wysokość podstawy

===: chyba niezbyt uważnie to analizujesz. H to wysokość ostrosłupa a x+y+z to szukana suma długości odcinków łączących prostą k z punktami przecięcia się jej ze ścianami bocznymi ostrosłupa