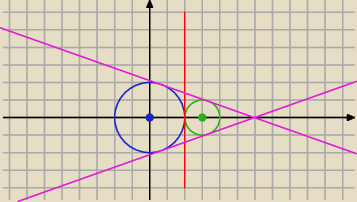
Znajdź równania wspólnych zewnętrznych stycznych do okręgów RiviT: Znajdź równania wspólnych zewnętrznych stycznych do okręgów: x2+y2=4 i (x−3)2+y2=1 Jedna to będzie x=2 Doszedłem do tego że przecięcia dwóch pozostałych stycznych jest (6,0). Wyszło mi to z trójkątów podobnych Jak to dalej ugryźć?

aniabb: z odległości punktu od prostej próbowałeś?

aniabb:

aniabb: x+2√2y−6=0 lub x−2√2y−6=0

RiviT: Czy coś to da skoro nie mam równania tej prostej? Ax+By+C=0 Podstawiając punkt który policzyłem dostaje; C=−6A CZYLI: Ax+By−6A=0 Jak podstawie do wzoru na odległość to mi się licznik wyzeruje

RiviT: współczynnik kierunkowy chciałem obliczyć z tangensa ale wyszło mi b= 2 lub −2

RiviT: edit: złe boki wziąłem do tangensa

aniabb: i podstaw C=−6A znów do którejś odległości i wylicz B i skróć potem A

RiviT: Coś mi nie wychodzi to bo dostaje coś takiego: http://i67.tinypic.com/2rrq7uo.jpg

aniabb: a to wstaw do tej drugiej bo tę już użyłeś

RiviT: Nie rozumiem o co Ci chodzi proszę o wyjaśnienie

aniabb: z drugiego okręgu

|C|
	=2 |−6A|=2√A2+B2
√A2+B2

RiviT: Rozumiem, dzięki