K Kasia: Ustal ile rozwiązań ma rownanie (x−3)²|sinxx|=sinx w przedziale <0;2π>

Bogdan: sinxx ? a to co?

Kasia: Przez przypadek, powinno być sinx

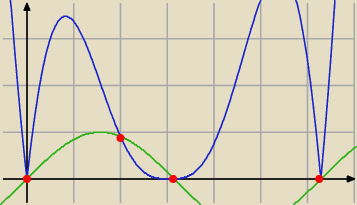
aniabb: 4 rozwiązania

Kasia: I skąd to się wzięło?

Bogdan:

	sinx
(x − 3)2 =		i |sinx| ≠ 0
	|sinx|

	sinx		sinx
Dla sin > 0:		=		= 1 i (x − 3)2 = 1
	|sinx|		sinx

	sinx		sinx
Dla sin < 0:		=		= −1 i (x − 3)2 = −1
	|sinx|		−sinx

Kontynuuj

Kasia: Zrobiłam tak i w przypadku, gdy sinx<0 wyszlo mi, ze nie ma pierwiastkow, a gdy wiekszy ta sa dwa, a odpowiedź to 4 😏

Kasia: Ponieważ tam wychodzi delta rowna 36−40, czyli mniejsza od 0

aniabb: dolicz jeszcze gdy sinx=0

aniabb: bo wtedy nie możesz dzielić

Kasia: Rozumiem, dziękuję