pochodne nie zdam matury: Znaleźć równanie prostej stycznej do wykresow funkcji f(x)=x²+1 i g(x)=(x−1)² −1 Trochę się gubię w tym zadaniu, nie wiem co z nim zrobić, mógłby ktoś wytłumaczyć metodę?

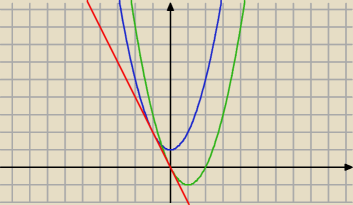
aniabb: czerwona y=−2x

Mila: Wspólna styczna: 1) styczna do wykresu: f(x)=x²+1 (x₀,x₀¹+1) − punkt styczności z wykresem f(x) s: y=f'(x₀)*(x−x₀)+f(x₀) f'(x)=2x f'(x₀)=2x₀ s: y= 2x₀*(x−x₀)+x₀²+1⇔y=2x₀*x−x₀²+1 2) g(x)=x²−2x g'(x)=2x−2 (x₁,g(x₁)− punkt styczności z wykresem funkcji g(x): s': y=(2x₁−2)*(x−x₁)+x₁²−2x₁⇔ y=(2x₁−2)*x−x₁² 3) skoro mają być styczna wspólna to: 2x₁−2=2x₀ −x₁²=−x₀²+1 x₁=0 i y₁=0 x₀=−1, y₀=2 4) f'(−1)=−2, Styczna: s: y=−2x Wg drugiego wzoru: ================== s': y=−2x

nie zdam matury: dziękuję!