Oblicz najwieksza objętość stożka o Pc=P Jewa: Rozpatrujemy wszystkie stożki, których pole powierzchni całkowitej jest równe P. Oblicz wysokość i promień podstawowy tego stożka, który ma największą objętość. Podaj te największą objętość.

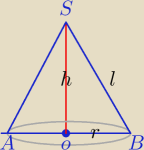
Mila: 1) P=πr²+πr*l P−πr²=π*r*l

	P−πr2		P
l=		=		−r
	π*r		πr

2)l²=r²+h²⇔

	P		P2		2P
r2+h2=(		−r)2⇔h2=		−
	πr		π2r2		π

3)

	1
V=		π*r2*h
	3

	1		π2		P2		2P
V2=		*π2*r4*h2 ⇔V2(r)=		*r4*(		−		)
	9		9		π2r2		π

	π2		P2r2		2P*r4
V2(r)=f(r)=		*(		−		)
	9		π2		π

	π2		2P2*r		8P*r3
f'(r)=		*(		−		)
	9		π2		π

	2P2*r		8P*r3
f'(r)=0⇔(		−		)=0, r>0⇔
	π2		π

	2p2		8r2
r*(		−		)=0
	π2		π

2P2		8r2
	−		) =0 /*π2 /:2
π2		π

P²−4P*πr²=0 P−4π*r²=0

	P
r2=
	4π

	√P		√P
r=		lub r=−		∉D
	2√π		2√π

	2P
h2=
	π

	√P
f'(r)>0 dla r∊(0,		⇔
	2

	√P
dla r=		funkcja f(r) ma największą wartość, w takim razie
	2

	√P
Vmax=V(		)
	2√π

	1		P		√2P		P√2P
Vmax=		π*		*		=
	3		4π		√π		12√π

============================

Mila: Posprawdzaj rachunki.