Czemu raz dziedziną funkcji jest zbiór liczb rzeczywistych a innym nie? signumy: Czemu raz dziedziną funkcji jest ℛ a innym razem nie? Proszę o wytłumaczenie na tych dwóch przykładach: a) f(x) = x−4 / |x−1|+3 b) f(x) = 3+x⁴ / |x+1|−2

aniabb: bo nie wolno dzielić przez 0 .. więc mianownik=0 wyrzucamy z dziedziny R

aniabb: nie wolno też wyciągać pierwiastków parzystego stopnia z ujemnych liczb ...więc pierwiastki też nakładają ograniczenia na dziedzinę

aniabb: a logarytmy sprawdź sam

aniabb: w Twoich a) |x−1|+3 ≠0 |x−1|≠ − 3 żaden x nie da −3 więc mogą być wszystkie czyli R b) |x−1|−2 ≠0 |x−1|≠2 x−1≠2 i x−1≠−2 x≠3 i x≠−1 więc dziedziną są R/{−1;3}

signumy: Dlaczego żaden x nie da −3?

aniabb: bo moduł pozbawia wszystkie wyniki minusa

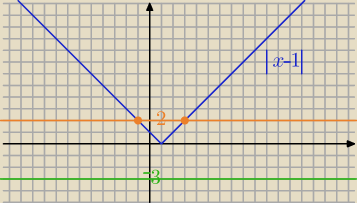
aniabb: albo bardziej obrazowo...kiedy niebieska przecina zieloną a przy okazji ... a kiedy żółtą ?

signumy: Zielonej nigdy, a żółtą w dwóch punktach. Teraz już rozumiem